题目内容
17.用40cm长的铁丝围成一个扇形,求此扇形面积的最大值.分析 设出圆的半径和弧长,由扇形的面积公式S扇形=$\frac{1}{2}$lr,得出关于半径的二次函数,由二次函数的顶点坐标得出扇形面积的最大值.
解答 解:设半径为r,弧长为l,则40=2r+l,
∴l=40-2r,
∴S扇形=$\frac{1}{2}$lr=$\frac{1}{2}$r (40-2r)=-r2+20r=-(r-10)2+100,
∴当半径为10时,扇形面积最大,最大值为100cm2.
点评 本题考查了扇形的面积公式,以及二次函数的最值问题,用扇形的半径表示成面积的二次函数是解题的关键.

练习册系列答案
相关题目
5.下列有理数的大小比较,正确的是( )
| A. | -2.9>3.1 | B. | -10>-9 | C. | -4.3<-3.4 | D. | 0<-20 |
2.如图,将一副三角尺按不同的位置摆放,下列方式中∠α与∠β互余的是( )


| A. | 图① | B. | 图② | C. | 图③ | D. | 图④ |
6.方程3x-6=0的解的相反数是( )
| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
 如图,已知线段AB的长为a,延长线段AB至点C,使BC=$\frac{1}{2}AB$.
如图,已知线段AB的长为a,延长线段AB至点C,使BC=$\frac{1}{2}AB$.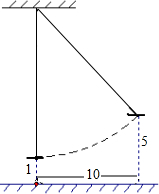 如图所示,有一架绳索拉直的秋千,当它静止时,踏板与地面的距离为1尺;将它往前推进10尺,踏板与地面的距离就为5尺.
如图所示,有一架绳索拉直的秋千,当它静止时,踏板与地面的距离为1尺;将它往前推进10尺,踏板与地面的距离就为5尺. 如图是由4个小正方体搭成的几何体,请你分别画出从正面、左面、上面看到的这个几何体的形状图.
如图是由4个小正方体搭成的几何体,请你分别画出从正面、左面、上面看到的这个几何体的形状图.