��Ŀ����
8��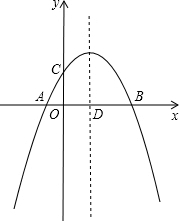 ��ͼ��������y=ax2+$\frac{3}{2}$x+c��a��0����x�ύ��A��B���㣬��y�ύ�ڵ�C�������ߵĶԳ��ύx���ڵ�D����֪��A������Ϊ��-1��0������C������Ϊ��0��2����
��ͼ��������y=ax2+$\frac{3}{2}$x+c��a��0����x�ύ��A��B���㣬��y�ύ�ڵ�C�������ߵĶԳ��ύx���ڵ�D����֪��A������Ϊ��-1��0������C������Ϊ��0��2������1���������ߵĽ���ʽ��
��2���������ߵĶԳ������Ƿ���ڵ�P��ʹ��PCD����CDΪ���ĵ��������Σ�������ڣ�ֱ��д��P������ꣻ��������ڣ���˵�����ɣ�
��3����E���߶�BC�ϵ�һ�����㣬����E��x��Ĵ������������ཻ�ڵ�F������E�˶���ʲôλ��ʱ���ı���CDBF������������ı���CDBF������������ʱE������꣮
���� ��1�����ô���ϵ����ת��Ϊ�ⷽ���鼴�ɣ�
��2����ͼ1�У��������������ۢٵ�CP=CDʱ���ڵ�DP=DCʱ���ֱ������P���꼴�ɣ�
��3����ͼ2�У���CM��EF��M����E��a��-$\frac{1}{2}a$+2����F��a��-$\frac{1}{2}$a2+$\frac{3}{2}$a+2������EF=-$\frac{1}{2}$a2+$\frac{3}{2}$a+2-��-$\frac{1}{2}a$+2��=-$\frac{1}{2}$a2+2a����0��a��4��������S�ı���CDBF=S��BCD+S��CEF+S��BEF=$\frac{1}{2}$•BD•OC+$\frac{1}{2}$•EF•CM+$\frac{1}{2}$•EF•BN���������κ��������ö��κ��������ʼ��ɽ�����⣮
��� �⣺��1��������$\left\{\begin{array}{l}{a-\frac{3}{2}+c=0}\\{c=2}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{c=2}\end{array}\right.$��
����κ����Ľ���ʽΪy=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2��
��2�����ڣ���ͼ1�У�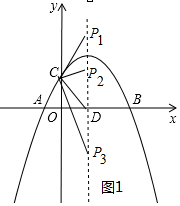
��C��0��2����D��$\frac{3}{2}$��0����
��CD=$\sqrt{{2}^{2}+��\frac{3}{2}��^{2}}$=$\frac{5}{2}$��
��CP=CDʱ��P1��$\frac{3}{2}$��4����
��DP=DCʱ��P2��$\frac{3}{2}$��$\frac{5}{2}$����P3��$\frac{3}{2}$��-$\frac{5}{2}$����
�������������������ĵ�P����Ϊ��$\frac{3}{2}$��4����$\frac{3}{2}$��$\frac{5}{2}$����$\frac{3}{2}$��-$\frac{5}{2}$����
��3����ͼ2�У���CM��EF��M��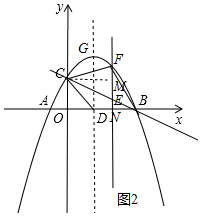
��B��4��0����C��0��2����
��ֱ��BC�Ľ���ʽΪy=-$\frac{1}{2}x+2$����E��a��-$\frac{1}{2}a$+2����F��a��-$\frac{1}{2}$a2+$\frac{3}{2}$a+2����
��EF=-$\frac{1}{2}$a2+$\frac{3}{2}$a+2-��-$\frac{1}{2}a$+2��=-$\frac{1}{2}$a2+2a����0��a��4����
��S�ı���CDBF=S��BCD+S��CEF+S��BEF=$\frac{1}{2}$•BD•OC+$\frac{1}{2}$•EF•CM+$\frac{1}{2}$•EF•BN
=$\frac{5}{2}$+$\frac{1}{2}$a��-$\frac{1}{2}$a2+2a��+$\frac{1}{2}$��4-a����-$\frac{1}{2}$a2+2a��
=-a2+4a+$\frac{5}{2}$
=-��a-2��2+$\frac{13}{2}$��
��a=2ʱ���ı���CDBF�����������ֵΪ$\frac{13}{2}$��
��E��2��1����
���� ���⿼����κ����ۺ��⡢һ�κ�����Ӧ�á�����ϵ�������ı��ε������֪ʶ������Ĺؼ���ѧ���÷������۵�˼��˼�����⣬ѧ�ṹ�����κ��������ֵ���⣬�����п�ѹ���⣮

 �¸��̵�ѧϵ�д�
�¸��̵�ѧϵ�д� ����ͬѧһ����ʦȫ�źþ�ϵ�д�
����ͬѧһ����ʦȫ�źþ�ϵ�д�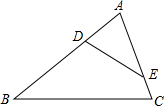 ��ͼ���ڡ�ABC�У���D��AB���ϣ���E��AC���ϣ��ҡ�AED=��B����AE=3��EC=1��AD=2����AB�ij���
��ͼ���ڡ�ABC�У���D��AB���ϣ���E��AC���ϣ��ҡ�AED=��B����AE=3��EC=1��AD=2����AB�ij���
 ����һ��ƽ��ֱ������ϵ��������ϵ�������x��ľ������3��y��ľ������4�����е㣬��д����Щ��֮��ĶԳƹ�ϵ��
����һ��ƽ��ֱ������ϵ��������ϵ�������x��ľ������3��y��ľ������4�����е㣬��д����Щ��֮��ĶԳƹ�ϵ�� ��ͼ����P�ڱ߳�Ϊ1��������ABCD��AD�ϣ�����PB������B��һ���������DC���ӳ��߽��ڵ�Q��ʹ�á�QBE=��PBC������E�DZ�AB�ӳ����ϵĵ㣬����PQ����PQ2=PB2+PD2+1�����PAB�����Ϊ$\frac{1}{4}$��
��ͼ����P�ڱ߳�Ϊ1��������ABCD��AD�ϣ�����PB������B��һ���������DC���ӳ��߽��ڵ�Q��ʹ�á�QBE=��PBC������E�DZ�AB�ӳ����ϵĵ㣬����PQ����PQ2=PB2+PD2+1�����PAB�����Ϊ$\frac{1}{4}$��