题目内容
20.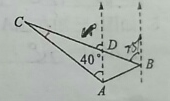 如图,C处在B处北偏西75°方向,C处在A处的北偏西40°方向,求∠ACB.
如图,C处在B处北偏西75°方向,C处在A处的北偏西40°方向,求∠ACB.
分析 根据方向角是视线与正南或正北方向的夹角,因而可以过A,B,两点分别作出正南正北方向的线,就可得到一组平行线,根据平行线的性质和三角形内角和的性质即可求解.
解答 解:如图,∠DAB+∠ABE=180°,
∵∠CBE=75°,
∴∠DAB+∠ABC=105°,
∵∠CAD=40°,
∴∠CAB+∠ABC=145°,
∴∠ACB=180°-145°=35°.
点评 本题主要考查了方向角的定义,熟练掌握方向角的问题与平行线、三角形内角和的性质的综合应用是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8. 如图,点O在直线AB上,∠COD=90°,若∠COA=36°,则∠DOB的度数是( )
如图,点O在直线AB上,∠COD=90°,若∠COA=36°,则∠DOB的度数是( )
 如图,点O在直线AB上,∠COD=90°,若∠COA=36°,则∠DOB的度数是( )
如图,点O在直线AB上,∠COD=90°,若∠COA=36°,则∠DOB的度数是( )| A. | 36° | B. | 54° | C. | 64° | D. | 72° |
5.在科学计算器上按顺序按3,8,×,1,5,+,3,2,=,最后屏幕上显示( )
| A. | 686 | B. | 602 | C. | 582 | D. | 502 |
9. 关于x的不等式$x-3>\frac{3x+a}{2}$的解集在数轴上表示如图所示,则a的值是( )
关于x的不等式$x-3>\frac{3x+a}{2}$的解集在数轴上表示如图所示,则a的值是( )
 关于x的不等式$x-3>\frac{3x+a}{2}$的解集在数轴上表示如图所示,则a的值是( )
关于x的不等式$x-3>\frac{3x+a}{2}$的解集在数轴上表示如图所示,则a的值是( )| A. | -6 | B. | -12 | C. | 6 | D. | 12 |
10.现有四根长3cm、4cm、7cm、9cm的木棒,任取其中的三根,首尾相连后,能组成三角形的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
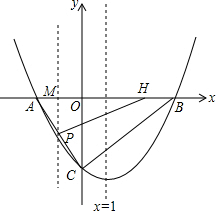 如图,在平面直角坐标系xoy中,抛物线y=ax2+bx-4与x轴交于点A(-2,0)和点B,与y轴交于点C,直线x=1是该抛物线的对称轴.
如图,在平面直角坐标系xoy中,抛物线y=ax2+bx-4与x轴交于点A(-2,0)和点B,与y轴交于点C,直线x=1是该抛物线的对称轴.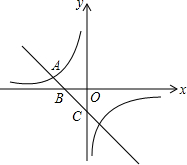 如图,反比例函数y=$\frac{k}{x}$图象与一次函数y=-x-1图象的一个交点为A(-2,a).
如图,反比例函数y=$\frac{k}{x}$图象与一次函数y=-x-1图象的一个交点为A(-2,a).