题目内容
 如图,已知半径OD与弦AB互相垂直,垂足为点C,若AB=8,CD=3,则⊙O的半径为( )
如图,已知半径OD与弦AB互相垂直,垂足为点C,若AB=8,CD=3,则⊙O的半径为( )| A、4 | ||
| B、5 | ||
C、
| ||
D、
|
考点:垂径定理,勾股定理
专题:
分析:连接OA,设⊙O的半径为r,则OC=r-3,再根据垂径定理求出AC的长,由勾股定理即可得出结论.
解答: 解:连接OA,设⊙O的半径为r,则OC=r-3,
解:连接OA,设⊙O的半径为r,则OC=r-3,
∵半径OD与弦AB互相垂直,AB=8,
∴AC=
AB=4.
在Rt△AOC中,OA2=OC2+AC2,即r2=(r-3)2+42,解得r=
.
故选C.
 解:连接OA,设⊙O的半径为r,则OC=r-3,
解:连接OA,设⊙O的半径为r,则OC=r-3,∵半径OD与弦AB互相垂直,AB=8,
∴AC=
| 1 |
| 2 |
在Rt△AOC中,OA2=OC2+AC2,即r2=(r-3)2+42,解得r=
| 25 |
| 6 |
故选C.
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
化简
的结果为( )
| (tan60°-1)2 |
A、1-
| ||||
B、1-
| ||||
C、
| ||||
D、
|
在-25,0,
,2.5这四个数中,绝对值最大的数是( )
| 2 |
| 5 |
| A、-25 | ||
| B、0 | ||
C、
| ||
| D、2.5 |
下列事件中,为必然事件的是( )
| A、某射击运动员射击一次,命中靶心 |
| B、经过城市中某一有交通信号的路口,遇到红灯 |
| C、抛掷一枚硬币,正面向上 |
| D、掷一枚骰子,点数大于0 |
下列计算正确的是( )
| A、a2•a2=2a2 |
| B、a4+a2=2 |
| C、(-ab)2=a2b2 |
| D、(2a2)3=6a6 |
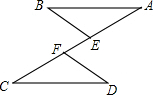 如图,已知AB∥CD,AE=CF,则下列条件:①AB=CD;②BE∥DF;③∠B=∠D;④BE=DF.其中不一定能使△ABE≌△CDF的是
如图,已知AB∥CD,AE=CF,则下列条件:①AB=CD;②BE∥DF;③∠B=∠D;④BE=DF.其中不一定能使△ABE≌△CDF的是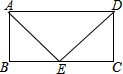 如图,在矩形ABCD中,E为BC的中点,且∠AED=90°,AD=10,则AB的长为
如图,在矩形ABCD中,E为BC的中点,且∠AED=90°,AD=10,则AB的长为