题目内容
18.如图1,点D、B、C、E在同一条直线上,在△ABC中,∠BAC=40°,AB=AC=2,点D、E在直线BC上由左向右运动,且始终保持∠DAE=110°,当点D向点B运动时(D不与B重合),如图(2),设DB=x,CE=y,则y与x的函数关系的图象大致可以表示为( )
| A. |  | B. |  | C. |  | D. |  |
分析 利用AB=AC可得∠ABC=∠ACB,进而可得∠ABD=∠ACE,然后证明∠ADB=∠CAE,可得△ADB∽△EAC,根据相似三角形的对应边成比例可得y与x之间的函数关系式,从而作出判断.
解答 解:∵AB=AC,∠BAC=40°,
∴∠ABC=∠ACB=70°,
∴∠ABD=∠ACE,∠ADB+∠BAD=70°,
∵∠DAE=110°,
∴∠BAD+∠CAE=70°,
∴∠ADB=∠CAE,
∴△ADB∽△EAC,
∴$\frac{DB}{AC}=\frac{AB}{EC}$,
∴xy=4,
解得y=$\frac{4}{x}$.
故选:A.
点评 本题主要考查了相似三角形的判定与性质和函数的图象,利用两角对应相等得到两三角形相似是解决本题的关键.

练习册系列答案
相关题目
9.若关于x的不等式组$\left\{\begin{array}{l}{3x-2<7}\\{x<a}\end{array}\right.$的解集是x<3,则下列结论正确的是( )
| A. | a=3 | B. | a≤3 | C. | a>3 | D. | a≥3 |
10.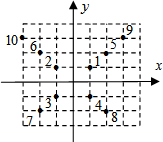 如图,在一坐标平面上,1在(1,1)位置,将自然数由小到大,由内而外,依逆时针方向排列在正方形的各顶点,那么数字159的位置在( )
如图,在一坐标平面上,1在(1,1)位置,将自然数由小到大,由内而外,依逆时针方向排列在正方形的各顶点,那么数字159的位置在( )
 如图,在一坐标平面上,1在(1,1)位置,将自然数由小到大,由内而外,依逆时针方向排列在正方形的各顶点,那么数字159的位置在( )
如图,在一坐标平面上,1在(1,1)位置,将自然数由小到大,由内而外,依逆时针方向排列在正方形的各顶点,那么数字159的位置在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.下列各组中,是同类项的是( )
| A. | 2与52 | B. | 2abc与-3ac | C. | -2xy与-2ab | D. | 3x2y与3xy2 |
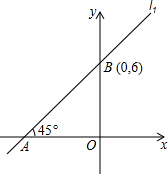 如图,平面直角坐标系中画出了函数l1:y1=kx+b的图象.
如图,平面直角坐标系中画出了函数l1:y1=kx+b的图象.
 如图,在矩形纸片ABCD中,AB=6cm,点E在BC上,且AE=CE,若将纸片沿AE折叠,点B恰好与AC上的点B1重合,则AC=12cm.
如图,在矩形纸片ABCD中,AB=6cm,点E在BC上,且AE=CE,若将纸片沿AE折叠,点B恰好与AC上的点B1重合,则AC=12cm.