题目内容
2. 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=6,DE=2,则△BCE的面积等于6.
如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=6,DE=2,则△BCE的面积等于6.
分析 作EF⊥BC于F,根据角平分线的性质求得EF=DE=2,然后根据三角形面积公式求得即可.
解答  解:作EF⊥BC于F,
解:作EF⊥BC于F,
∵BE平分∠ABC,EF⊥BC,ED⊥AB,
∴EF=DE=2,
∴△BCE的面积=$\frac{1}{2}$×BC×EF=6.
故答案为:6.
点评 本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
相关题目
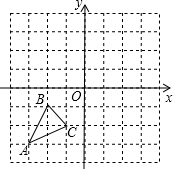 如图,已知A(-3,-3),B(-2,-1),C(-1.-2)是坐标平面上三点.
如图,已知A(-3,-3),B(-2,-1),C(-1.-2)是坐标平面上三点. 如图,△ABC是等边三角形,P是CB延长线上一点,Q是BC延长线上一点,且满足∠PAQ=120°.求证:BC2=PB•QC.
如图,△ABC是等边三角形,P是CB延长线上一点,Q是BC延长线上一点,且满足∠PAQ=120°.求证:BC2=PB•QC.