题目内容
已知过原点O的两直线与圆心为M(0,4),半径为2的圆相切,切点分别为P、Q,PQ交y轴于点K,抛物线经过P、Q两点,顶点为N(0,6),且与x轴交于A、B两点.

(1)求点P的坐标;
(2)求抛物线解析式;
(3)在直线y=nx+m中,当n=0,m≠0时,y=m是平行于x轴的直线,设直线y=m与抛物线相交于点C、D,当该直线与⊙M相切时,求点A、B、C、D围成的多边形的面积(结果保留根号).

(1)求点P的坐标;
(2)求抛物线解析式;
(3)在直线y=nx+m中,当n=0,m≠0时,y=m是平行于x轴的直线,设直线y=m与抛物线相交于点C、D,当该直线与⊙M相切时,求点A、B、C、D围成的多边形的面积(结果保留根号).
考点:二次函数综合题,解一元二次方程-直接开平方法,待定系数法求二次函数解析式,等腰三角形的性质,勾股定理,切线的性质,切线长定理
专题:代数几何综合题
分析:(1)由切线的性质可得∠MPO=90°,根据勾股定理可求出PO,然后由面积法可求出PK,然后运用勾股定理可求出OK,就可得到点P的坐标.
(2)可设顶点为(0,6)的抛物线的解析式为y=ax2+6,然后将点P的坐标代入就可求出抛物线的解析式.
(3)直线y=m与⊙M相切有两种可能,只需对这两种情况分别讨论就可求出对应多边形的面积.
(2)可设顶点为(0,6)的抛物线的解析式为y=ax2+6,然后将点P的坐标代入就可求出抛物线的解析式.
(3)直线y=m与⊙M相切有两种可能,只需对这两种情况分别讨论就可求出对应多边形的面积.
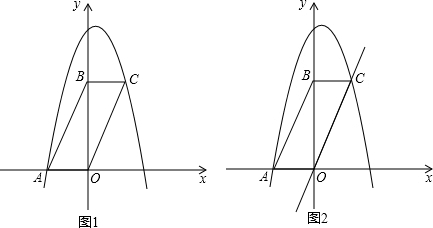
解答:解:(1)如图1,

∵⊙M与OP相切于点P,
∴MP⊥OP,即∠MPO=90°.
∵点M(0,4)即OM=4,MP=2,
∴OP=2
.
∵⊙M与OP相切于点P,⊙M与OQ相切于点Q,
∴OQ=OP,∠POK=∠QOK.
∴OK⊥PQ,QK=PK.
∴PK=
=
=
.
∴OK=
=3.
∴点P的坐标为(
,3).
(2)如图2,
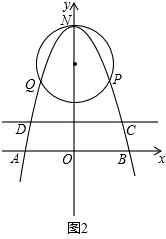
设顶点为(0,6)的抛物线的解析式为y=ax2+6,
∵点P(
,3)在抛物线y=ax2+6上,
∴3a+6=3.
解得:a=-1.
则该抛物线的解析式为y=-x2+6.
(3)当直线y=m与⊙M相切时,
则有
=2.
解得;m1=2,m2=6.
①m=2时,如图3,
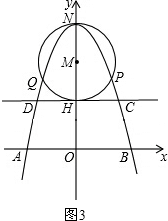
则有OH=2.
当y=2时,解方程-x2+6=2得:x=±2,
则点C(2,2),D(-2,2),CD=4.
同理可得:AB=2
.
则S梯形ABCD=
(DC+AB)•OH=
(4+2
)×2=4+2
.
②m=6时,如图4,
此时点C、点D与点N重合.
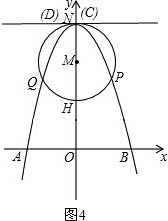
S△ABC=
AB•OC=
×2
×6=6
.
综上所述:点A、B、C、D围成的多边形的面积为4+2
或6
.

∵⊙M与OP相切于点P,
∴MP⊥OP,即∠MPO=90°.
∵点M(0,4)即OM=4,MP=2,
∴OP=2
| 3 |
∵⊙M与OP相切于点P,⊙M与OQ相切于点Q,
∴OQ=OP,∠POK=∠QOK.
∴OK⊥PQ,QK=PK.
∴PK=
| PM•PO |
| OM |
2×2
| ||
| 4 |
| 3 |
∴OK=
| OP2-PK2 |
∴点P的坐标为(
| 3 |
(2)如图2,

设顶点为(0,6)的抛物线的解析式为y=ax2+6,
∵点P(
| 3 |
∴3a+6=3.
解得:a=-1.
则该抛物线的解析式为y=-x2+6.
(3)当直线y=m与⊙M相切时,
则有
|
解得;m1=2,m2=6.
①m=2时,如图3,

则有OH=2.
当y=2时,解方程-x2+6=2得:x=±2,
则点C(2,2),D(-2,2),CD=4.
同理可得:AB=2
| 6 |
则S梯形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 6 |
| 6 |
②m=6时,如图4,
此时点C、点D与点N重合.

S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 6 |
| 6 |
综上所述:点A、B、C、D围成的多边形的面积为4+2
| 6 |
| 6 |
点评:本题考查了用待定系数法求二次函数的解析式、圆的切线的性质、切线长定理、等腰三角形的性质、勾股定理、解一元二次方程等知识,有一定的综合性,难度适中,容易漏掉多边形为三角形的这一情况.

练习册系列答案
相关题目
设A(x1,y1),B(x2,y2)是正比例函数y=-2x图象上的两点,若x1<x2<0,则y1与y2之间的关系是( )
| A、y2<y1<0 |
| B、y1<y2<0 |
| C、y2>y1>0 |
| D、y1>y2>0 |
下列性质中,菱形具有,矩形不一定具有的是( )
| A、四个角为直角 |
| B、对角线互相垂直 |
| C、对角线相等 |
| D、对角相等 |
 如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.
如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.