题目内容
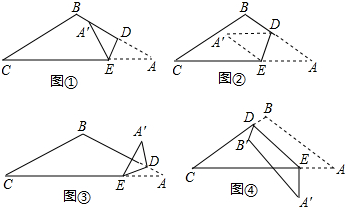
(1)如图①,将△ABC纸片沿DE(点D、E分别在AB和AC上)进行折叠,当点A落在四边形BCED的边BD上时,请直接写出∠A与∠CEA′之间的数量关系是 ;
(2)如图②,将△ABC纸片沿DE(点D、E分别在AB和AC上)进行折叠,当点A落在四边形BCED的内部时,直接写出∠A与∠CEA′、∠BDA′之间的数量关系是 ;
(3)如图③,将△ABC纸片沿DE(点D、E分别在AB和AC上)进行折叠,当点A落在四边形BCED的外部时,写出∠A与∠CEA′、∠BDA′之间的数量关系,并说明理由;
(4)如图④,如果将△ABC纸片沿DE(点D在BC上,点E在AC上)进行折叠,当点A落在△ABC的外部,点B落在△CDE的内部时,请你直接写出∠A、∠B与∠CEA′、∠CDB′之间的数量关系是 .
(2)如图②,将△ABC纸片沿DE(点D、E分别在AB和AC上)进行折叠,当点A落在四边形BCED的内部时,直接写出∠A与∠CEA′、∠BDA′之间的数量关系是
(3)如图③,将△ABC纸片沿DE(点D、E分别在AB和AC上)进行折叠,当点A落在四边形BCED的外部时,写出∠A与∠CEA′、∠BDA′之间的数量关系,并说明理由;
(4)如图④,如果将△ABC纸片沿DE(点D在BC上,点E在AC上)进行折叠,当点A落在△ABC的外部,点B落在△CDE的内部时,请你直接写出∠A、∠B与∠CEA′、∠CDB′之间的数量关系是

考点:三角形内角和定理,三角形的外角性质,翻折变换(折叠问题)
专题:
分析:(1)根据翻折的性质可得∠A=∠DA′E,然后根据三角形的一个外角等于与它不相邻的两个内角的和解答即可;
(2)根据翻折变换的性质,运用三角形的内角和定理即可解决问题.
(3)借助翻折变换的性质,运用三角形的内角和定理即可解决问题.
(4)借助翻折变换的性质,运用四边形形的内角和等于360°这一结论即可解决问题.
(2)根据翻折变换的性质,运用三角形的内角和定理即可解决问题.
(3)借助翻折变换的性质,运用三角形的内角和定理即可解决问题.
(4)借助翻折变换的性质,运用四边形形的内角和等于360°这一结论即可解决问题.
解答: 解:(1)如图1,∠CEA′=2∠A.
解:(1)如图1,∠CEA′=2∠A.
(2)如图2,∠CEA′+∠BDA′=2∠A.
(3)如图3,∠CEA′-∠BDA′=2∠A.证明如下:由题意得:∠A′ED=∠AED(设为α),∠A′DE=∠ADE(设为β);
∵∠CEA′+2α=180°,∠BDA′=β-∠BDE
=β-(∠A+α),
∴∠CEA′-∠BDA′
=180°-(α+β)+∠A;
∵∠A=180°-(α+β),
∴∠CEA′-∠BDA′=2∠A.
(4)如图4,2∠A+2∠B-∠CDB′-∠CEA′=360°
 解:(1)如图1,∠CEA′=2∠A.
解:(1)如图1,∠CEA′=2∠A.(2)如图2,∠CEA′+∠BDA′=2∠A.
(3)如图3,∠CEA′-∠BDA′=2∠A.证明如下:由题意得:∠A′ED=∠AED(设为α),∠A′DE=∠ADE(设为β);
∵∠CEA′+2α=180°,∠BDA′=β-∠BDE
=β-(∠A+α),
∴∠CEA′-∠BDA′
=180°-(α+β)+∠A;
∵∠A=180°-(α+β),
∴∠CEA′-∠BDA′=2∠A.
(4)如图4,2∠A+2∠B-∠CDB′-∠CEA′=360°
点评:本题考查了翻折变换的性质,三角形的一个外角等于与它不相邻的两个内角的和,三角形的内角和等于180°,综合题,但难度不大,熟记性质准确识图是解题的关键.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
抛物线y=-2x2+1向右平移1个单位,再向上平移1个单位后所得到的抛物线为( )
| A、y=-2(x+1)2-2 |
| B、y=-2(x+1)2+2 |
| C、y=-2(x-1)2-2 |
| D、y=-2(x-1)2+2 |
 我国古代数学家赵爽的“勾股方圆图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是25,小正方形的面积是1,直角三角形的两直角边分别是a和b,那么(a+b)2的值为
我国古代数学家赵爽的“勾股方圆图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是25,小正方形的面积是1,直角三角形的两直角边分别是a和b,那么(a+b)2的值为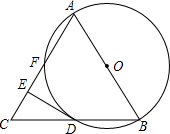 如图,△ABC中,AB=AC,以AB为直径的⊙O,交BC于D点交AC于F点,过点D作DE⊥AC,垂足为E.
如图,△ABC中,AB=AC,以AB为直径的⊙O,交BC于D点交AC于F点,过点D作DE⊥AC,垂足为E.
 如图,△ABC是边长为4cm的等边三角形,P是△ABC内的任意一点,过点P作EF∥AB分别交AC,BC于点E,F,作GH∥BC分别交AB,AC于点G,H,作MN∥AC分别交AB,BC于点M,N,试猜想:EF+GH+MN的值是多少?其值是否随P位置的改变而变化?并说明你的理由.
如图,△ABC是边长为4cm的等边三角形,P是△ABC内的任意一点,过点P作EF∥AB分别交AC,BC于点E,F,作GH∥BC分别交AB,AC于点G,H,作MN∥AC分别交AB,BC于点M,N,试猜想:EF+GH+MN的值是多少?其值是否随P位置的改变而变化?并说明你的理由.