题目内容
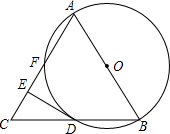 如图,△ABC中,AB=AC,以AB为直径的⊙O,交BC于D点交AC于F点,过点D作DE⊥AC,垂足为E.
如图,△ABC中,AB=AC,以AB为直径的⊙O,交BC于D点交AC于F点,过点D作DE⊥AC,垂足为E.(1)求证:
 |
| BD |
 |
| DF |
(2)求证:DE为⊙O的切线;
(3)若CE=2,∠BAC=60°,求由DC、CF与
 |
| DF |
考点:切线的判定,扇形面积的计算
专题:
分析:(1)根据圆周角的性质求得∠ADB=90°,∠DAC=∠DBF,根据等腰三角形的性质求得∠CAD=∠BAD,从而求得∠BAD=∠DBF,即可求得
=
;
(2)连接OD,先求得OD三角形的中位线,从而求得OD∥AC,即可求得OD⊥DE,从而求得DE为⊙O的切线;
(3)连接OF,先求得四边形BCFO是菱形,从而求得∠C=∠FOD=60°,然后根据S=S四边形BCFO-S扇形DOF即可求得由DC、CF与
所围成图形的面积S.
 |
| BD |
 |
| DF |
(2)连接OD,先求得OD三角形的中位线,从而求得OD∥AC,即可求得OD⊥DE,从而求得DE为⊙O的切线;
(3)连接OF,先求得四边形BCFO是菱形,从而求得∠C=∠FOD=60°,然后根据S=S四边形BCFO-S扇形DOF即可求得由DC、CF与
 |
| DF |
解答: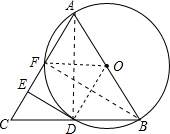 (1)证明:连接AD,BF,
(1)证明:连接AD,BF,
∵AB为⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵AB=AC,
∴∠CAD=∠BAD,
∵∠DAC=∠DBF,
∴∠BAD=∠DBF
∴
=
;
(2)证明:连接OD,
∵AB为⊙O的直径,
∴AO=BO,
∵AD⊥BC,AB=AC,
∴CD=DB,
∴OD是△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∵OD是半径,
∴DE为⊙O的切线;
(3)解:连接OF,
∵AB=AC,OF=OA,∠BAC=60°,
∴△ABC、△AFO都是等边三角形,
∴∠AFO=∠C=60°,
∴OF∥CD,
∵OD∥AC,
∴四边形BCFO是平行四边形,
∵OB=OF,
∴四边形BCFO是菱形,
∴∠C=∠FOD=60°,
OD=DC=CF,
∵DE⊥AC,
∴DC=2CE=4=OD=CF,
∴DE=
=2
,
∴S=S四边形BCFO-S扇形DOF=CF•DE-
=4×2
-
=8
-
π.
 (1)证明:连接AD,BF,
(1)证明:连接AD,BF,∵AB为⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵AB=AC,
∴∠CAD=∠BAD,
∵∠DAC=∠DBF,
∴∠BAD=∠DBF
∴
 |
| BD |
 |
| DF |
(2)证明:连接OD,
∵AB为⊙O的直径,
∴AO=BO,
∵AD⊥BC,AB=AC,
∴CD=DB,
∴OD是△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∵OD是半径,
∴DE为⊙O的切线;
(3)解:连接OF,
∵AB=AC,OF=OA,∠BAC=60°,
∴△ABC、△AFO都是等边三角形,
∴∠AFO=∠C=60°,
∴OF∥CD,
∵OD∥AC,
∴四边形BCFO是平行四边形,
∵OB=OF,
∴四边形BCFO是菱形,
∴∠C=∠FOD=60°,
OD=DC=CF,
∵DE⊥AC,
∴DC=2CE=4=OD=CF,
∴DE=
| CD2-CE2 |
| 3 |
∴S=S四边形BCFO-S扇形DOF=CF•DE-
| nπr2 |
| 360 |
| 3 |
| 60π×42 |
| 360 |
| 3 |
| 8 |
| 3 |
点评:本题考查了切线的性质和判定,圆周角的性质,等边三角形的判定,菱形的判定以及扇形的面积等,作出辅助线是本题的关键.

练习册系列答案
相关题目
要锻造一个直径为100mm,高为80mm的圆柱形钢坯,应截取直径为80mm的圆钢( )
| A、120mm |
| B、125mm |
| C、130mm |
| D、135mm |
 实数a、b在数轴上的对应点如图所示,则下列不等式中错误的是( )
实数a、b在数轴上的对应点如图所示,则下列不等式中错误的是( )| A、a+b<0 | ||
| B、ab<0 | ||
| C、a-b<0 | ||
D、
|
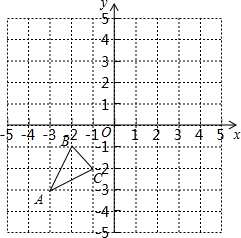 如图已知A(-3,-3),B(-2,-1),C(-1,-2)是直角坐标平面上三点.
如图已知A(-3,-3),B(-2,-1),C(-1,-2)是直角坐标平面上三点. 如图,数轴上点A所表示的数为1,点B,C,D是4×4的正方形网格上的格点,以点A为圆心,AD长为半径画圆交数轴于P,Q两点,则P点所表示的数为
如图,数轴上点A所表示的数为1,点B,C,D是4×4的正方形网格上的格点,以点A为圆心,AD长为半径画圆交数轴于P,Q两点,则P点所表示的数为