题目内容
2.从1、2、3这三个数字中,任意抽取两个不同数字组成一个两位数,则这个两位数能被3整除的概率是$\frac{1}{3}$.分析 先画树状图展示所有6种等可能的结果数,再找出这个两位数能被3整除的结果数,然后根据概率公式求解.
解答 解:画树状图为:
共有6种等可能的结果数,其中这个两位数能被3整除的结果数为2,所以这个两位数能被3整除的概率=$\frac{2}{6}$=$\frac{1}{3}$.
故答案为$\frac{1}{3}$.
点评 本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.

练习册系列答案
相关题目
13.下列说法正确的是( )
| A. | 0是绝对值最小的有理数 | |
| B. | 绝对值等于本身的数只能是正数 | |
| C. | 数轴上原点两侧的数互为相反数 | |
| D. | 两个数比较大小,绝对值大的反而小 |
17.用配方法解一元二次方程x2+6x-8=0时可配方得( )
| A. | (x-3)2=17 | B. | (x+3)2=17 | C. | (x-3)2=1 | D. | (x-3)2=-1 |
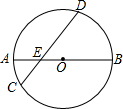 如图,AB是⊙O的直径切AB=8,CD是弦,CD交AB于E,且E为OA的中点,∠BED=45°,
如图,AB是⊙O的直径切AB=8,CD是弦,CD交AB于E,且E为OA的中点,∠BED=45°,