题目内容
15.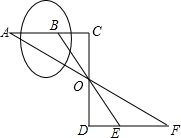 如图,某人要测量河中浅滩B和对岸A的距离,先在岸边定出点C,使C、A、B在一直线上,再在AC的垂直方向在岸边画线段CD,取它的中点O,又画DF⊥CD,观测E、O、B在一直线上,同时F、O、A也在一直线上,那么EF的长就是浅滩B和对岸A的距离,为什么?
如图,某人要测量河中浅滩B和对岸A的距离,先在岸边定出点C,使C、A、B在一直线上,再在AC的垂直方向在岸边画线段CD,取它的中点O,又画DF⊥CD,观测E、O、B在一直线上,同时F、O、A也在一直线上,那么EF的长就是浅滩B和对岸A的距离,为什么?
分析 利用全等三角形的判定方法得出△BOC≌△EOD,进而得出△AOC≌△FDO,进而得出答案.
解答 解:在△BOC和△EOD中
$\left\{\begin{array}{l}{∠C=∠D}\\{CO=DO}\\{∠COB=∠DOE}\end{array}\right.$,
∴△BOC≌△EOD(ASA),
∴BC=DE,
在△AOC和△FDO中
$\left\{\begin{array}{l}{∠C=∠D}\\{CO=DO}\\{∠AOC=∠FOD}\end{array}\right.$,
∴△AOC≌△FDO(ASA),
∴AC=DF,
∴AB=EF,
即EF的长就是浅滩B和对岸A的距离.
点评 此题主要考查了全等三角形的应用,正确利用全等三角形的判定方法是解题关键.

练习册系列答案
相关题目
20.点P在第四象限,点P到x轴的距离是4,到y轴的距离是2,则点P的坐标是( )
| A. | (4,2) | B. | (4,-2) | C. | (-2,4) | D. | (2,-4) |
 如图,点A(-3,0),B(0,2),将三角形AOB向右平移5个单位长度,再向下平移2个单位长度得到三角形CDE,点A、O、B的对应点分别为C、D、E.点P从点O开始水平向右平移,点Q从点D开始水平向左平移,速度均为每秒2个单位长度,运动时间为t秒.
如图,点A(-3,0),B(0,2),将三角形AOB向右平移5个单位长度,再向下平移2个单位长度得到三角形CDE,点A、O、B的对应点分别为C、D、E.点P从点O开始水平向右平移,点Q从点D开始水平向左平移,速度均为每秒2个单位长度,运动时间为t秒.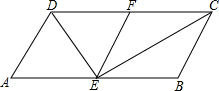 在四边形ABCD中,AD=BC,DE平分∠ADF,CE平分∠BCF,∠CDE+∠DCE=90°,E,F分别是AB,CD的中点.
在四边形ABCD中,AD=BC,DE平分∠ADF,CE平分∠BCF,∠CDE+∠DCE=90°,E,F分别是AB,CD的中点.