题目内容
1.已知函数y=(k+$\frac{1}{2}$)${x}^{{k}^{2}-3}$(k为常数).(1)当k为何值时,该函数是正比例函数;
(2)当k为何值时,正比例函数y随x的增大而增大;
(3)当k为何值时,正比例函数y随x的增大而减少;
(4)分别作出它们的图象;
(5)点A(2,5)与点B(2,-3)分别在哪条直线上?
分析 (1)由正比例函数的定义得到方程组解得即可;
(2)由正比例函数的性质即可得到结论;
(3)由正比例函数的性质即可得到结论;
(4)过(0,0),(1,k)作直线可得函数的图象;
(5)把A(2,5),B(2,-3)分别代入函数的解析式可知点在哪条直线上.
解答 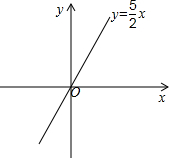 解:(1)当$\left\{\begin{array}{l}{{k}^{2}-3=1}\\{k+\frac{1}{2}≠0}\end{array}\right.$,解得:k=±2,
解:(1)当$\left\{\begin{array}{l}{{k}^{2}-3=1}\\{k+\frac{1}{2}≠0}\end{array}\right.$,解得:k=±2,
∴当k=±2时,该函数是正比例函数;
∴正比例函数的解析式为:y=$\frac{5}{2}$x,或y=-$\frac{3}{2}$x;
(2)由(1)得,当k=2时,正比例函数y随x的增大而增大;
(3)由(1)得,当k=-2时,正比例函数y随x的增大而减少;
(4)如图所示:
(5)把x=2,代入y=$\frac{5}{2}$x,y=-$\frac{3}{2}$x中,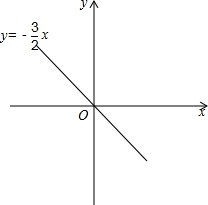
得y=5,或y=-3,
∴A(2,5)在y=$\frac{5}{2}$x上,B(2,-3)在y=-$\frac{3}{2}$x上.
点评 本题考查了正比例函数的性质,一次函数的定义,正比例函数的图象,一次函数图象上点的特征,熟记函数的定义是解题的关键.

练习册系列答案
相关题目
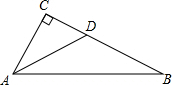 如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,CD=5cm,则BD的长是10cm.
如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,CD=5cm,则BD的长是10cm.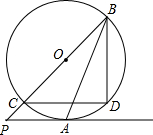 如图,PA与⊙O相切于点A,弦CD∥PA,CB为⊙O直径,且P、C、B共线.
如图,PA与⊙O相切于点A,弦CD∥PA,CB为⊙O直径,且P、C、B共线.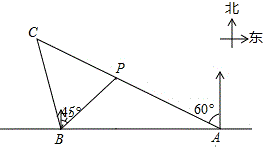 如图,在一笔直的海岸线l上有A、B两个观测站,A在B的正东方向,AB=8$\sqrt{6}$km,有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向,小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向,求点C与点B之间的距离(结果保留根号).
如图,在一笔直的海岸线l上有A、B两个观测站,A在B的正东方向,AB=8$\sqrt{6}$km,有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向,小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向,求点C与点B之间的距离(结果保留根号).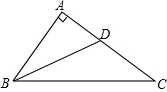 如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,若AB=4,且点D到BC的距离为3,则BD=5.
如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,若AB=4,且点D到BC的距离为3,则BD=5.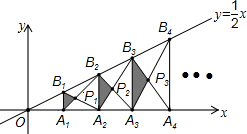 如图,已知A1,A2,A3,…,An,An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1,A2,A3,…,An,An+1作x轴的垂线交直线y=$\frac{1}{2}$x于点B1,B2,B3,…,Bn,Bn+1,连接A1B2,B1A2,A2B3,B2A3,…,AnBn+1,BnAn+1,依次相交于点P1,P2,P3,…,Pn,△A1B1P1,△A2B2P2,…,△AnBnPn的面积依次记为S1,S2,S3,…,Sn,则Sn=$\frac{{n}^{2}}{8n+4}$(请用含n的代数式表示).
如图,已知A1,A2,A3,…,An,An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1,A2,A3,…,An,An+1作x轴的垂线交直线y=$\frac{1}{2}$x于点B1,B2,B3,…,Bn,Bn+1,连接A1B2,B1A2,A2B3,B2A3,…,AnBn+1,BnAn+1,依次相交于点P1,P2,P3,…,Pn,△A1B1P1,△A2B2P2,…,△AnBnPn的面积依次记为S1,S2,S3,…,Sn,则Sn=$\frac{{n}^{2}}{8n+4}$(请用含n的代数式表示).