题目内容
16.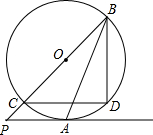 如图,PA与⊙O相切于点A,弦CD∥PA,CB为⊙O直径,且P、C、B共线.
如图,PA与⊙O相切于点A,弦CD∥PA,CB为⊙O直径,且P、C、B共线.(1)求证:BA平分∠CBD;
(2)若∠OAB=30°,CD=6$\sqrt{3}$,求OA.
分析 (1)连接AO,由PA与⊙O相切于点A,得到OA⊥PA,根据CD∥PA,推出OA⊥CD,由垂径定理得到$\widehat{AC}$=$\widehat{AD}$,证出∠1=∠2,得到BA平分∠CBD;
(2)由同圆的半径相等得到∠1=∠OAB=30°,由CB为⊙O直径,得到∠D=90°,求出直径,结论可求.
解答 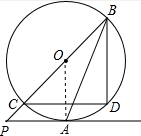 (1)证明:连接AO,
(1)证明:连接AO,
∵PA与⊙O相切于点A,
∴OA⊥PA,
∵CD∥PA,
∴OA⊥CD,
∴$\widehat{AC}$=$\widehat{AD}$,
∴∠1=∠2,
∴BA平分∠CBD;
(2)∵OA=OB,∠OAB=30°,
∴∠1=∠OAB=30°,
∴∠CBD=60°,
∵CB为⊙O直径,
∴∠D=90°,
∵CD=6$\sqrt{3}$,
∴BC=12,
∴OA=$\frac{1}{2}$BC=6.
点评 本题考查了切线的性质,平行线的性质,圆周角定理,解直角三角形,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
8.下列说法中,正确的是( )
| A. | 同位角相等 | B. | 内错角相等 | C. | 同旁内角相等 | D. | 对顶角相等 |
6.若分式$\frac{x-2}{x+1}$无意义,则x的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
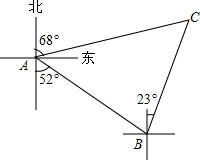 如图,某轮船航行至A处测得灯塔C位于北偏东68°的方向上,若该轮船从A处以每小时18海里的速度沿南偏东52°方向匀速航行,1小时候到达码头B,此时测得灯塔C位于北偏东23°方向上.
如图,某轮船航行至A处测得灯塔C位于北偏东68°的方向上,若该轮船从A处以每小时18海里的速度沿南偏东52°方向匀速航行,1小时候到达码头B,此时测得灯塔C位于北偏东23°方向上.