题目内容
 有一块三角形土地,它的底边BC=48米,高AH=16米,某单位要沿着底边BC修座底面积是矩形DEFG的大楼.当这个大楼地基面积为192平方米时,这个矩形的长和宽各是多少?
有一块三角形土地,它的底边BC=48米,高AH=16米,某单位要沿着底边BC修座底面积是矩形DEFG的大楼.当这个大楼地基面积为192平方米时,这个矩形的长和宽各是多少?考点:相似三角形的应用
专题:
分析:两三角形相似,对应高之比等于相似比.利用此性质即可解答.
解答: 解:∵DE∥BC
解:∵DE∥BC
∴△ADG∽△ABC
它们的对应高线比等于对应线段的比,
即
=
,
设AM=x,那么DG=MH=AH-AM=16-x
∴
=
,
∴DG=3x
∴S四边形DEFG=DG•DE=(16-x)•3x=192,
解得:x=8,
∴DG=16-x=8,DE=3x=24
∴矩形的长和宽分别是24m和8m.
 解:∵DE∥BC
解:∵DE∥BC∴△ADG∽△ABC
它们的对应高线比等于对应线段的比,
即
| AM |
| AH |
| DE |
| BC |
设AM=x,那么DG=MH=AH-AM=16-x
∴
| x |
| 16 |
| DE |
| 48 |
∴DG=3x
∴S四边形DEFG=DG•DE=(16-x)•3x=192,
解得:x=8,
∴DG=16-x=8,DE=3x=24
∴矩形的长和宽分别是24m和8m.
点评:此题考查了相似三角形的性质,解答时既要利用相似三角形的性质,又要利用一元二次方程的应用,有一定难度.

练习册系列答案
相关题目
展览馆有A,B两个入口,D、E、F三个出口,则从A入口进,F出口出的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
西瓜每千克1元,买50千克以上按8折优惠,甲、乙两人所买西瓜的重量不同可付的钱相同,若甲买48千克,则乙买的西瓜重量是( )
| A、48千克 | B、84千克 |
| C、64千克 | D、60千克 |
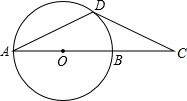 如图,点D是半径为R的⊙O上一点.
如图,点D是半径为R的⊙O上一点.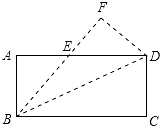 如图,矩形ABCD中,BC=8,AB=4,将矩形纸片沿对角线对折,使C点落在F处,BC与AD边交于点E.
如图,矩形ABCD中,BC=8,AB=4,将矩形纸片沿对角线对折,使C点落在F处,BC与AD边交于点E.