题目内容
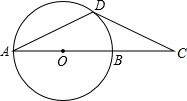 如图,点D是半径为R的⊙O上一点.
如图,点D是半径为R的⊙O上一点.(1)若∠A=∠C=30°,求证:直线CD与⊙O相切;
(2)已知直线CD与⊙O相切,下列条件:①AD=CD;②∠A=30°;③∠ADC=120°;④DC=
| 3 |
考点:切线的判定与性质
专题:
分析:(1)连接OD;由∠A=∠C=30°,证出∠ODC=90°,即可证明直线CD与⊙O相切;
(2)由AD=CD,OA=OD,得出∠A=∠C=∠ODA,再由CD是⊙O的切线,得出∠ODC=90°,即可证出∠C=30°,得出BC=OD=R.
(2)由AD=CD,OA=OD,得出∠A=∠C=∠ODA,再由CD是⊙O的切线,得出∠ODC=90°,即可证出∠C=30°,得出BC=OD=R.
解答:解:(1)连接OD;如图所示: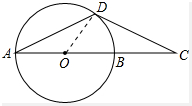
∵∠A=∠C=30°,
∴∠ADC=120°,
∵OA=OD,
∴∠ODA=∠A=30°,
∴∠ODC=120°-30°=90°,
∴直线CD与⊙O相切;
(2)能得出BC=R的是①②③④;
∵AD=CD,OA=OD,
∴∠A=∠C,∠A=∠ODA,
∴∠A=∠C=∠ODA,
∴∠DOC=∠A+∠ODA=2∠C,
∵CD是⊙O的切线,
∴∠ODC=90°,
∴∠DOC+∠C=90°,
∴3∠C=90°,
∴∠C=30°,
∴OC=2OD,
∴BC=OD=R.

∵∠A=∠C=30°,
∴∠ADC=120°,
∵OA=OD,
∴∠ODA=∠A=30°,
∴∠ODC=120°-30°=90°,
∴直线CD与⊙O相切;
(2)能得出BC=R的是①②③④;
∵AD=CD,OA=OD,
∴∠A=∠C,∠A=∠ODA,
∴∠A=∠C=∠ODA,
∴∠DOC=∠A+∠ODA=2∠C,
∵CD是⊙O的切线,
∴∠ODC=90°,
∴∠DOC+∠C=90°,
∴3∠C=90°,
∴∠C=30°,
∴OC=2OD,
∴BC=OD=R.
点评:本题考查了切线的判定与性质以及含30°角的直角三角形的性质;熟练掌握切线的判定与性质是解题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
如图图形中,不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 有一块三角形土地,它的底边BC=48米,高AH=16米,某单位要沿着底边BC修座底面积是矩形DEFG的大楼.当这个大楼地基面积为192平方米时,这个矩形的长和宽各是多少?
有一块三角形土地,它的底边BC=48米,高AH=16米,某单位要沿着底边BC修座底面积是矩形DEFG的大楼.当这个大楼地基面积为192平方米时,这个矩形的长和宽各是多少?