题目内容
9.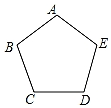 如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(-3,2),(b,m),(c,m),则点E的坐标是(3,2).
如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(-3,2),(b,m),(c,m),则点E的坐标是(3,2).
分析 根据题意得出y轴位置,进而利用正多边形的性质得出E点坐标.
解答  解:如图所示:∵A(0,a),
解:如图所示:∵A(0,a),
∴点A在y轴上,
∵C,D的坐标分别是(b,m),(c,m),
∴B,E点关于y轴对称,
∵B的坐标是:(-3,2),
∴点E的坐标是:(3,2).
故答案为:(3,2).
点评 此题主要考查了正多边形和圆,正确得出y轴的位置是解题关键.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
17.如果代数式3x2-4x的值为6,那么6x2-8x-9的值为( )
| A. | 12 | B. | 3 | C. | $\frac{3}{2}$ | D. | -3 |
14.在50包型号为L的衬衫的包裹中混进了型号为M的衬衫,每包20件衬衫,每包中混入的M号衬衫数如表:
根据以上数据,选择正确选项( )
| M号衬衫数 | 0 | 1 | 4 | 5 | 7 | 9 | 10 | 11 |
| 包数 | 7 | 3 | 10 | 15 | 5 | 4 | 3 | 3 |
| A. | M号衬衫一共有47件 | |
| B. | 从中随机取一包,包中L号衬衫数不低于9是随机事件 | |
| C. | 从中随机取一包,包中L号衬衫数不超过4的概率为0.26 | |
| D. | 将50包衬衫混合在一起,从中随机拿出一件衬衫,恰好是M号的概率为0.252 |
18.在△ABC中,∠C=90°,AB=6,cosA=$\frac{1}{3}$,则AC等于( )
| A. | 18 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{1}{18}$ |
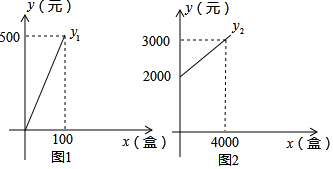
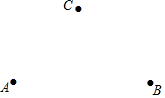 按照下列要求完成作图及问题解答.
按照下列要求完成作图及问题解答.