题目内容
11.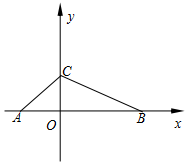 如图,在平面直角坐标系中,△ABC 的顶点坐标分别为A(-2,0)、B(4,0)、C(0,2).
如图,在平面直角坐标系中,△ABC 的顶点坐标分别为A(-2,0)、B(4,0)、C(0,2).(1)请用尺规作出△ABC的外接圆⊙P(保留作图痕迹,不写作法);
(2)求出(1)中外接圆圆心P的坐标;
(3)若点C的坐标改为(0,a),其余条件不变,是否存在这样的点C使得∠ACB=45°?如果存在,请直接写出a的值;如果不存在,请说明理由.
分析 (1)作AC和AB线段的垂直平分线交于点P,则点P即为△ABC的外接圆的圆心;
(2)根据(1)可知:直线EF是线段AB的垂直平分线,则直线EF的解析式为:x=1,因为点P一定在直线EF上,所以点P的横坐标为1,设P(1,y),根据PA=PC及两点的距离公式列方程解出即可;
(3)如图3,存在,如图3,当点C在y轴的正半轴时,则a>0,构建△ABC的外接圆⊙P,由∠ACB=45°,可知圆心角∠ACB=90°,则点P的坐标为(1,3),根据两点距离公式代入PA=PC中列方程可解出a的值,同理在y轴的负半轴上也有一点C符合条件,且a=-3-$\sqrt{17}$.
解答 解:(1)如图1,画△ABC的外接圆⊙P;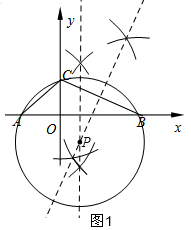
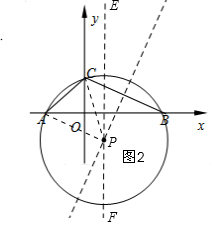
(2)如图2,∵A(-2,0)、B(4,0),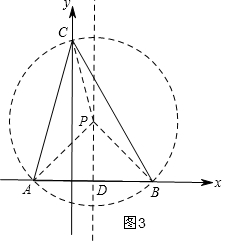
∴AB=4,直线EF的解析式为:x=1,
∴P的横坐标为1,
设P(1,y),
由PA=PC得:(1+2)2+(y-0)2=(1-0)2+(y-2)2,
解得:y=-1,
∴P(1,-1);
(3)存在,
如图3,当点C在y轴的正半轴时,则a>0,
作△ABC的外接圆⊙P,连接PA、PB、PC,过P作PD⊥x轴于D,
∴AD=BD,
∴AP=PB,
∵∠ACB=45°,
∴∠APB=90°,
∴∠PAB=∠PBA=45°,
∴△PAD是等腰直角三角形,
∴AD=PD,
∵A(-2,0)、B(4,0),
∴P(1,3),
∵PA=PC,
则(1+2)2+(3-0)2=(1-0)2+(3-a)2,
解得:a1=3+$\sqrt{17}$,x2=3-$\sqrt{17}$(舍),
同理,在y轴的负半轴上还存在一点C,则a=-3-$\sqrt{17}$,
综上所述,a的值为3+$\sqrt{17}$或-3-$\sqrt{17}$.
点评 本题是三角形的综合题,考查了三角形的外接圆,明确三边垂直平分线的交点就是三角形外接圆的圆心,叫外心,此题的解题思路为:①构建三角形的外接圆,利用45°的圆周角得到90°的圆心角,求外接圆圆心的坐标,②根据同圆的半径相等和两点距离公式列式求解.

| A. | 1:2 | B. | $\sqrt{3}$:3 | C. | 1:3 | D. | 不能确定 |
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y2<y1 | D. | y2<y1<y3 |
| A. | 三角形三条高的交点 | B. | 三角形三条内角平分线的交点 | ||
| C. | 三角形三条中线的交点 | D. | 无法确定 |
| A. | (-3-2)2 | B. | (-3)×(-2)4 | C. | (-3)4÷(-4)3 | D. | (-3)3×(-$\frac{1}{2}$)2 |
| A. | (-3,2) | B. | (3,2) | C. | (-3,-2) | D. | (3,-2) |
| A. | $\left\{\begin{array}{l}{x=4}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=5}\\{y=-1}\end{array}\right.$ |
| A. | x1=x2=4 | B. | x1=x2=0 | C. | x1=4,x2=0 | D. | x1=2,x2=-2 |
| A. | 顶点作标为(-3,2) | B. | 对称轴为:直线x=-3 | ||
| C. | 当x≥3时y随x增大而减小 | D. | 函数的最小值是2 |