题目内容
13.下列说法正确的是( )| A. | 一个游戏中奖的概率是$\frac{1}{500}$,则做500次这样的游戏一定会中奖 | |
| B. | 了解50发炮弹的杀伤半径,应采用普查的方式 | |
| C. | 一组数据1,2,3,2,3的众数和中位数都是2 | |
| D. | 数据:1,3,5,5,6的方差是3.2 |
分析 分别利用概率的意义以及抽样调查的意义以及众数和中位数求法,以及方差求法先求平均数,再代入公式S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2]计算即可.
解答 解:A、一个游戏中奖的概率是$\frac{1}{500}$,则做500次这样的游戏一定会中奖,错误;
B、了解50发炮弹的杀伤半径,应采用抽样调查的方式,故此选项错误;
C、一组数据1,2,3,2,3的众数是2,3,中位数是2,故、此选项错误;
D、$\overline{x}$=(1+3+5+5+6)÷5=4,
S2=$\frac{1}{5}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],
=$\frac{1}{5}$[(1-4)2+(3-4)2+(5-4)2+(5-4)2+(6-4)2]
=3.2;
故选:D.
点评 本题考查了概率的意义以及抽样调查的意义以及众数和中位数、方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.

练习册系列答案
相关题目
18.20150的值是( )
| A. | 2015 | B. | 0 | C. | 1 | D. | -1 |
5.若代数式$\frac{\sqrt{x}}{x-2}$有意义,则实数x的取值范围是( )
| A. | x≠2,x≠1 | B. | x≥0 | C. | x>0 | D. | x≥0且x≠2 |
3.下列计算正确的是( )
| A. | (-14)-(+5)=-19 | B. | 0-(-3)=0 | C. | (-3)-(-3)=-6 | D. | |5-3|=-(5-3) |
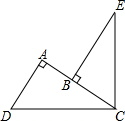 如图,∠DCE=90°,∠DAC=90°,BE⊥AC于点B,且DC=EC,请证明:AB+AD=BE.
如图,∠DCE=90°,∠DAC=90°,BE⊥AC于点B,且DC=EC,请证明:AB+AD=BE.
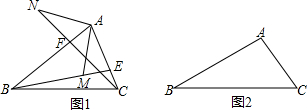
 如图,△ABC∽△AED,AD=5cm,EC=3cm,AC=10cm,则AB=14cm.
如图,△ABC∽△AED,AD=5cm,EC=3cm,AC=10cm,则AB=14cm.