题目内容
7. 在梯形ABCD中,AD∥BC,AD<BC,在BC上取一点E,使BE等于其中位线的长,证明:AC⊥BD,当且仅当ED也等于其中位线的长.
在梯形ABCD中,AD∥BC,AD<BC,在BC上取一点E,使BE等于其中位线的长,证明:AC⊥BD,当且仅当ED也等于其中位线的长.
分析 延长BC至点F使CF=AD,证得四边形ABCD为平行四边形,可得AC∥DF,由ED=$\frac{1}{2}(AD+BC)$=$\frac{1}{2}$BF,可得ED=EB=EF,由等腰三角形的性质和三角形内角和定理可得∠1+∠2+∠3+∠EDF=180°,等量代换证得∠2+∠EDF=90°,得AC⊥BD,反之结论也成立.
解答  证明:延长BC至点F使CF=AD,则AD+BC=CF+BC=BF,
证明:延长BC至点F使CF=AD,则AD+BC=CF+BC=BF,
则BE=$\frac{1}{2}(AD+BC)=\frac{1}{2}(CF+BC)$=$\frac{1}{2}BF$,
∵AD∥BC,
∴AD∥CF,
又∵AD=CF,
∴四边形ABCD为平行四边形,
∴AC∥DF,
若ED=$\frac{1}{2}(AD+BC)$=$\frac{1}{2}$BF,
则ED=EB=EF,
∴∠1=∠2,∠3=∠EDF,
∴∠1+∠2+∠3+∠EDF=180°,
2∠2+2∠EDF=180°,
∠2+∠EDF=90°,
∴∠BDF=90°,
∴∠BOC=90°,
即AC⊥BD,
反之,若AC⊥BD,即∠BDC=90°,
∵AC∥DF,
∴∠BDF=∠BDC=90°,
又∵E点为BF的中点,
∴DE=$\frac{1}{2}BF=\frac{1}{2}(AD+BC)$,
∴结论成立.
点评 本题主要考查了梯形的中位线的应用,能根据梯形的中位线求出AD+BC=2EF是解此题的关键,注意:梯形的中位线平行于两底,并且等于两底和的一半.

练习册系列答案
相关题目
19.下列根式中,与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{18}$ | C. | $\root{3}{2}$ | D. | $\sqrt{20}$ |
 如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=3.则矩形对角线的长等于6.
如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=3.则矩形对角线的长等于6.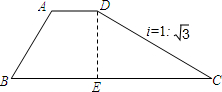 如图,梯形ABCD是拦水坝的横断面图,图中斜坡CD的坡度i=1:$\sqrt{3}$,∠B=60°,AB=6,AD=4,拦水坝的横断面ABCD的面积30$\sqrt{3}$.
如图,梯形ABCD是拦水坝的横断面图,图中斜坡CD的坡度i=1:$\sqrt{3}$,∠B=60°,AB=6,AD=4,拦水坝的横断面ABCD的面积30$\sqrt{3}$. 将两个直角三角形按图中方式叠放,则角α的度数等于75°.
将两个直角三角形按图中方式叠放,则角α的度数等于75°.