题目内容
10. 如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=35°,则∠BAC的度数为( )
如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=35°,则∠BAC的度数为( )| A. | 45° | B. | 40° | C. | 60° | D. | 70° |
分析 首先由AE∥BD,根据平行线的性质,求得∠DBC的度数,然后由BD平分∠ABC,求得∠ABC的度数,再由AB=AC,利用等边对等角的性质,求得∠C的度数,继而求得答案.
解答 解:∵AE∥BD,
∴∠DBC=∠E=35°,
∵BD平分∠ABC,
∴∠ABC=2∠DBC=70°,
∵AB=AC,
∴∠C=∠ABC=70°,
∴∠BAC=180°-∠ABC-∠C=40°.
故选B.
点评 此题考查了等腰三角形的性质、平行线的性质以及角平分线的定义.注意等边对等角定理的应用.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
18.如果$\frac{1}{3}$x2-2n-1=0是关于x的一元一次方程,那么n的值为( )
| A. | 0 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
5.与-2ab是同类项的为( )
| A. | -2ac | B. | $\frac{{2{x^2}y}}{3}$ | C. | ab | D. | -2abc |
2.在2、(-2)3、-5%、0、$-\frac{3}{7}$、|-2.3|这六个数中,非正数有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
19.把方程2-$\frac{3x+2}{3}$=-$\frac{x-5}{6}$去分母后,正确的是( )
| A. | 12-(3x+2)=-(x-5) | B. | 12-2(3x+2)=-x-5 | C. | 2-2(3x+2)=-(x-5) | D. | 12-2(3x+2)=-(x-5) |
 用小立方块搭一个几何体,如图所示,这样的几何体最少需要9个小立方块,最多需要13个小立方块.
用小立方块搭一个几何体,如图所示,这样的几何体最少需要9个小立方块,最多需要13个小立方块.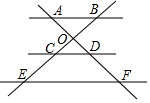 如图,AB∥CD∥EF,AF与BE相交于点O,则下列结论中正确的个数是( )
如图,AB∥CD∥EF,AF与BE相交于点O,则下列结论中正确的个数是( )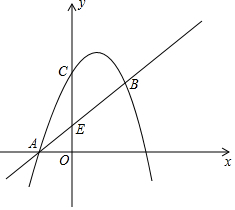 已知A(-1,0),B(2,3),C(0,3)三点在同一抛物上,该抛物线的顶点为D,直线AB与抛物线的对称轴的交点为E
已知A(-1,0),B(2,3),C(0,3)三点在同一抛物上,该抛物线的顶点为D,直线AB与抛物线的对称轴的交点为E