题目内容
20.若$\frac{1}{3}{a}^{2n-1}{b}^{2}$与-5b2a5是同类项,则n=3.分析 直接利用同类项的定义得出关于n的等式进而得出答案.
解答 解:∵$\frac{1}{3}{a}^{2n-1}{b}^{2}$与-5b2a5是同类项,
∴2n-1=5,
解得:n=3.
故答案为:3.
点评 此题主要考查了同类项,正确把握定义是解题关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
10. 如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=35°,则∠BAC的度数为( )
如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=35°,则∠BAC的度数为( )
 如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=35°,则∠BAC的度数为( )
如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=35°,则∠BAC的度数为( )| A. | 45° | B. | 40° | C. | 60° | D. | 70° |
11.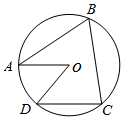 如图,A、B、C、D四个点均在⊙O上,∠AOD=50°,AO∥DC,则∠B的度数为( )
如图,A、B、C、D四个点均在⊙O上,∠AOD=50°,AO∥DC,则∠B的度数为( )
 如图,A、B、C、D四个点均在⊙O上,∠AOD=50°,AO∥DC,则∠B的度数为( )
如图,A、B、C、D四个点均在⊙O上,∠AOD=50°,AO∥DC,则∠B的度数为( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
15.在平面直角坐标系中,点(2,3)关于x轴对称的点是( )
| A. | (2,-3) | B. | (-2,3) | C. | (-2,-3 ) | D. | (3,2) |
5.解方程$3x+\frac{2x-1}{3}=3-\frac{x+1}{2}$时,去分母正确的是( )
| A. | 18x+2(2x-1)=18-3(x+1) | B. | 3x+2(2x-1)=3-3(x+1) | ||
| C. | 9x+(2x-1)=6-(x+1) | D. | 3x+(2x-1)=3-(x+1) |
12.代数式$\frac{1}{2a}$,4xy,$\frac{a+b}{3}$,a,2016,$\frac{1}{2}$a2b,-$\frac{3mn}{4}$中,单项式的个数有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
5.一个个位是4的三位数,如果把这个数4换到百位上,原来百位上的数换到十位,原来十位上的数换到个位上,所得的数比原数的3倍还多98,则原数是( )
| A. | 544 | B. | 144 | C. | 104 | D. | 404 |
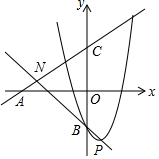 问题探究:
问题探究: