题目内容
11.(1)观察下列各式:$\sqrt{2-\frac{2}{5}}$=$\sqrt{\frac{8}{5}}$=$\sqrt{\frac{4×2}{5}}$=2$\sqrt{\frac{2}{5}}$,则$\sqrt{2-\frac{2}{5}}$=2$\sqrt{\frac{2}{5}}$
$\sqrt{3-\frac{3}{10}}$=$\sqrt{\frac{27}{10}}$=$\sqrt{\frac{9×3}{10}}$=3$\sqrt{\frac{3}{10}}$,则$\sqrt{3-\frac{3}{10}}$=3$\sqrt{\frac{3}{10}}$
(2)按照你发现的规律填空:
$\sqrt{4-\frac{4}{17}}$=$\sqrt{\frac{64}{17}}$=$\sqrt{\frac{16×4}{17}}$=4$\sqrt{\frac{4}{17}}$,则$\sqrt{4-\frac{4}{17}}$=4$\sqrt{\frac{4}{17}}$.
(3)猜想$\sqrt{5-\frac{5}{26}}$等于多少?
(4)请你用含有自然数n(n≥2)的式子写出你发现的规律.
分析 (2)根据算术平方根的概念进行计算;
(3)根据计算过程和各式的变化规律猜想结果;
(4)根据给出各式的计算过程和结果,总结规律.
解答 解:(2)$\sqrt{4-\frac{4}{17}}$=$\sqrt{\frac{64}{17}}$=$\sqrt{\frac{16×4}{17}}$=4$\sqrt{\frac{4}{17}}$,则$\sqrt{4-\frac{4}{17}}$=4$\sqrt{\frac{4}{17}}$;
(3)$\sqrt{5-\frac{5}{26}}$=5$\sqrt{\frac{5}{26}}$;
(4)$\sqrt{n+1-\frac{n+1}{n(n+2)+2}}$=(n+1)$\sqrt{\frac{n+1}{n(n+2)+2}}$.
点评 本题考查的是算术平方根的性质和数字的变化类知识,掌握算术平方根的概念、从给出的式子中正确找出规律是解题的关键.

练习册系列答案
相关题目
19.关于式子(-5)3,正确的说法是( )
| A. | -5是底数,3是幂 | B. | 5是底数,3是幂 | ||
| C. | 5是底数,3是指数 | D. | -5是底数,3是指数 |
16.开学初,学校食堂领导为了满足需要,去某米商处购买大米,已知每袋大米的标准重量为50千克,30袋大米的称重如下(超出的记为“+”,不足的记为“-”):
(1)与标准重量比较,30袋大米总计超过了多少千克或不足多少千克?
(2)30袋大米的总重量是多少千克?
(3)与标准质量相比不足或者超过1.5千克的包装都是不合格的,请问这30袋大米中有多少袋式包装不合格的?
| -1.6 | -1.2 | -1 | 0 | 1.2 | 1.4 | 1.8 |
| 1 | 5 | 4 | 8 | 6 | 4 | 2 |
(2)30袋大米的总重量是多少千克?
(3)与标准质量相比不足或者超过1.5千克的包装都是不合格的,请问这30袋大米中有多少袋式包装不合格的?
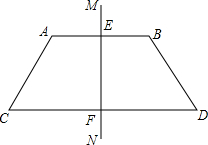 如图,MN垂直平分线段AB,CD,垂足分别为E,F,求证:AC=BD,∠C=∠D.
如图,MN垂直平分线段AB,CD,垂足分别为E,F,求证:AC=BD,∠C=∠D.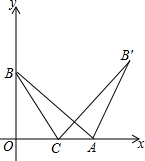 如图,在平面直角坐标系xOy中,点A、B分别在x轴,y轴的正半轴上,且OA=OB,将线段AB绕点A顺时针旋转60°得到AB′,C是x轴上一点,BC+B′C的值最小是B′D,∠OCB=60°.
如图,在平面直角坐标系xOy中,点A、B分别在x轴,y轴的正半轴上,且OA=OB,将线段AB绕点A顺时针旋转60°得到AB′,C是x轴上一点,BC+B′C的值最小是B′D,∠OCB=60°.