题目内容
11．
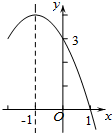二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，对称轴为直线x=-1，与x轴的一个交点为（1，0），与y轴的交点为（0，3），则方程ax2+bx+c=0（a≠0）的解为x1=1，x2=-3．
分析 直接利用抛物线的对称性以及结合对称轴以及抛物线y=ax2+bx+c与x轴的一个交点是（1，0），得出另一个与x轴的交点，进而得出答案．
解答 解：∵抛物线y=ax2+bx+c与x轴的一个交点是（1，0），对称轴为直线x=-1，
∴抛物线y=ax2+bx+c与x轴的另一个交点是（-3，0），
∴方程ax2+bx+c=0（a≠0）的解为：x1=1，x2=-3．
故答案为：x1=1，x2=-3．
点评 此题主要考查了抛物线与x轴的交点，正确得出抛物线与x轴的交点坐标是解题关键．
练习册系列答案
相关题目
2．二次函数y=ax2+bx+c（a≠0）图象上部分点的坐标（x，y）对应值列表如表：
则该函数图象的对称轴是直线x=-2．
| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y | … | -3 | -2 | -3 | -6 | -11 | … |
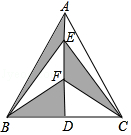如图，在等边三角形ABC中，AD是BC边上的高，点E、F是AD上的 两点，AB=8cm，AD=4$\sqrt{3}$cm，则图中阴影部分的面积是8$\sqrt{3}$cm．
如图，在△ABC中，AD是它的角平分线，AB：AC=8：5，则CD：BD=5：8．
1．下列各式中与$\sqrt{6}$是同类二次根式的是（ ）
| A． | $\sqrt{12}$ | B． | $\sqrt{\frac{2}{3}}$ | C． | $\sqrt{60}$ | D． | $\sqrt{18}$ |