题目内容
5. 一个由若干个小正方体组成的几何体,从左面看到的视图和从上面看到的视图如图所示,则该几何体最少需要5小正方体;最多可以有7小正方体.
一个由若干个小正方体组成的几何体,从左面看到的视图和从上面看到的视图如图所示,则该几何体最少需要5小正方体;最多可以有7小正方体.
分析 (1)由俯视图可得最底层的几何体的个数,由左视图第二层正方形的个数可得第二层最少需要几块正方体,相加即可得到该几何体最少需要几块小正方体;
(2)由俯视图和左视图可得第二层最多需要几块小正方体,再加上最底层的正方体的个数即可得到最多可以有几块小正方体.
解答 解:俯视图中有4个正方形,那么组合几何体的最底层有4个正方体,
(1)由左视图第二层有1个正方形可得组合几何体的第二层最少有1个正方体,
所以该几何体最少需要4+1=5块小正方体;
(2)俯视图从上边数第一行的第二层最多可有3个正方体,
所以该几何体最多需要4+3=7块小正方体.
故答案为:5,7.
点评 此题考查由三视图判断几何体;用到的知识点为:俯视图正方形的个数为组合几何体最底层的正方体的个数;左视图第二层正方形的个数为组合几何体第二层的正方体最少的个数.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
10.某型号的手机连续两次降价,每个售价由原来的1225元降到了625元,设平均每次降价的百分率为x,列出方程正确的是( )
| A. | 625(1+x)2=1225 | B. | 1225(1+x)2=625 | C. | 625(1-x)2=1225 | D. | 1225(1-x)2=625 |
14.若(x-1)2+$\sqrt{x+y}$=0,则x2016+y2017的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
15.目前节能灯在各城市已基本普及,今年某市面向县级及农村地区推广,为响应号召,朝阳灯饰商场用了4200元购进甲型和乙型两种节能灯.这两种型号节能灯的进价、售价如表:
特别说明:毛利润=售价-进价
(1)朝阳灯饰商场销售甲型节能灯一只毛利润是5元;
(2)朝阳灯饰商场购买甲,乙两种节能灯共100只,其中买了甲型节能灯多少只?
(3)现在朝阳灯饰商场购进甲型节能灯m只,销售完节能灯时所获的毛利润为y元.
①当y=1080时,求m的值;
②朝阳灯饰商场把购进的这两种型号节能灯全部销售完时,所获得的毛利润最多是1400元.(请直接写出答案)
| 进价(元/只) | 售价(元/只) | |
| 甲型 | 25 | 30 |
| 乙型 | 45 | 60 |
(1)朝阳灯饰商场销售甲型节能灯一只毛利润是5元;
(2)朝阳灯饰商场购买甲,乙两种节能灯共100只,其中买了甲型节能灯多少只?
(3)现在朝阳灯饰商场购进甲型节能灯m只,销售完节能灯时所获的毛利润为y元.
①当y=1080时,求m的值;
②朝阳灯饰商场把购进的这两种型号节能灯全部销售完时,所获得的毛利润最多是1400元.(请直接写出答案)
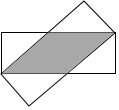 (如图所示)两个长宽分别为7cm、3cm的矩形如图叠放在一起,则图中阴影部分的面积是$\frac{87}{7}$cm2.
(如图所示)两个长宽分别为7cm、3cm的矩形如图叠放在一起,则图中阴影部分的面积是$\frac{87}{7}$cm2. 如图,AD是△ABC的中线,CE是△ACD的中线,S△AEC=3cm2,求S△ABC.
如图,AD是△ABC的中线,CE是△ACD的中线,S△AEC=3cm2,求S△ABC.