题目内容
3.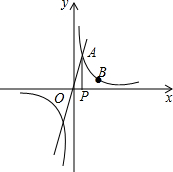 已知正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象交于点A,过点A作x轴的垂线,垂足为点P,已知△OAP的面积为1.
已知正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象交于点A,过点A作x轴的垂线,垂足为点P,已知△OAP的面积为1.(1)求反比例函数的解析式;
(2)有一点B的横坐标为2,且在反比例函数图象上,在x轴上存在一点M,使MA+MB最小,求点M的坐标.
分析 (1)设出A点的坐标,根据△OAP的面积为1,求出xy的值,得到反比例函数的解析式;
(2)作点A关于x轴的对称点A′,连接A′B,交x轴于点M,得到MA+MB最小时,点M的位置,求出直线A′B的解析式,得到它与x轴的交点,即点M的坐标.
解答 解:(1)设A点的坐标为(x,y),则OP=x,PA=y,
∵△OAP的面积为1,∴$\frac{1}{2}$xy=1,xy=2,即k=2,
∴反比例函数的解析式为:y=$\frac{2}{x}$.
(2)作点A关于x轴的对称点A′,连接A′B,交x轴于点M,MA+MB最小,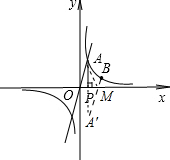
点B的横坐标为2,点B的纵坐标为y=$\frac{2}{2}$=1,
两个函数图象在第一象限的图象交于A点,
2x=$\frac{2}{x}$,x±1,y=±2,
A点的坐标(1,2),
A关于x轴的对称点A′(1,-2),
设直线A′B的解析式为y=kx+b,
$\left\{\begin{array}{l}{k+b=-2}\\{2k+b=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=3}\\{b=-5}\end{array}\right.$,
直线y=3x-5与x轴的交点为($\frac{5}{3}$,0),
则M点的坐标为($\frac{5}{3}$,0).
点评 本题考查的是反比例函数图象与一次函数图象的交点问题以及最短路线问题,解题的关键是确定MA+MB最小时,点M的位置,灵活运用数形结合思想求出有关点的坐标和图象的解析式路线解答.

练习册系列答案
相关题目
12.下列语句:
①正数与负数互为相反数;
②任何有理数都有相反数;
③一个数的相反数一定是负数,
正确的个数有( )
①正数与负数互为相反数;
②任何有理数都有相反数;
③一个数的相反数一定是负数,
正确的个数有( )
| A. | 0 个 | B. | 1个 | C. | 2 个 | D. | 3个 |
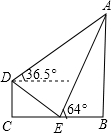 如图,某社区一建筑物上,悬挂“创文明小区,建和谐社会”的宣传条幅AB,小明站在位于建筑物正前方的台阶上D点处测得条幅顶端A的仰角为36.5°,朝着条幅的方向走到台阶下的E点处,测得条幅顶端A的仰角为64°,已知台阶DE的坡度为1:2,DC=2米,则条幅AB的长度为7.8米.
如图,某社区一建筑物上,悬挂“创文明小区,建和谐社会”的宣传条幅AB,小明站在位于建筑物正前方的台阶上D点处测得条幅顶端A的仰角为36.5°,朝着条幅的方向走到台阶下的E点处,测得条幅顶端A的仰角为64°,已知台阶DE的坡度为1:2,DC=2米,则条幅AB的长度为7.8米.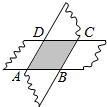 如图,用两张等宽的纸条交叉叠放在一起,重叠部分为四边形ABCD,它是一个特殊的四边形.
如图,用两张等宽的纸条交叉叠放在一起,重叠部分为四边形ABCD,它是一个特殊的四边形.