题目内容
7.菱形的两条对角线的长分别为6和8,则菱形的高为( )| A. | $\frac{24}{5}$ | B. | $\frac{48}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{12}{5}$ |
分析 根据对角线的长度即可计算菱形的面积,根据菱形对角线互相垂直平分的性质,可以求得△AOB为直角三角形,根据AO,BO可以求得AB的值,根据菱形的面积和边长即可解题.
解答 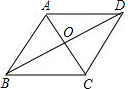 解:由题意知AC=6,BD=8,则菱形的面积S=$\frac{1}{2}$×6×8=24,
解:由题意知AC=6,BD=8,则菱形的面积S=$\frac{1}{2}$×6×8=24,
∵菱形对角线互相垂直平分,
∴△AOB为直角三角形,AO=3,BO=4,
∴AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=5,
∴菱形的高h=$\frac{S}{AB}$=$\frac{24}{5}$.
故选A.
点评 本题考查了勾股定理在直角三角形中的运用,菱形面积的计算,本题中求根据AO,BO的值求AB是解题的关键.

练习册系列答案
相关题目
17.下列说法错误的是( )
| A. | 三角形三条高交于三角形内一点 | |
| B. | 三角形三条中线交于三角形内一点 | |
| C. | 三角形三条角平分线交于三角形内一点 | |
| D. | 三角形的中线、角平分线、高都是线段 |
12.若a>b,则下列不等式变形正确的是( )
| A. | a+5<b+5 | B. | $\frac{a}{3}$<$\frac{b}{3}$ | C. | -4a>-4b | D. | 3a-2>3b-2 |