题目内容
4.计算下列各题:(1)8x2y4•(-$\frac{3x}{4{y}^{2}}$)•$\frac{6x}{{x}^{2}y}$;
(2)$\frac{a-1}{a-2}$÷$\frac{{a}^{2}-2a+1}{2a-4}$;
(3)$\frac{{x}^{2}-6x+9}{{x}^{2}-9}$÷$\frac{2x-6}{{x}^{2}+3x}$;
(4)(xy-x2)÷$\frac{{x}^{2}-2xy+{y}^{2}}{xy}$•$\frac{x-y}{{x}^{2}}$.
分析 (1)直接利用分式乘法运算法则化简求出即可;
(2)首先将分式的分子与分母分解因式,再利用分式除法运算法则进而化简即可;
(3)首先将分式的分子与分母分解因式,再利用分式除法运算法则进而化简即可;
(4)首先将分式的分子与分母分解因式,再利用分式乘除运算法则进而化简即可.
解答 解:(1)8x2y4•(-$\frac{3x}{4{y}^{2}}$)•$\frac{6x}{{x}^{2}y}$
=-8x2y4•$\frac{9}{2{y}^{3}}$
=-36x2y;
(2)$\frac{a-1}{a-2}$÷$\frac{{a}^{2}-2a+1}{2a-4}$
=$\frac{a-1}{a-2}$×$\frac{2(a-2)}{(a-1)^{2}}$
=$\frac{2}{a-1}$;
(3)$\frac{{x}^{2}-6x+9}{{x}^{2}-9}$÷$\frac{2x-6}{{x}^{2}+3x}$
=$\frac{(x-3)^{2}}{(x-3)(x+3)}$×$\frac{x(x+3)}{2(x-3)}$
=$\frac{x}{2}$;
(4)(xy-x2)÷$\frac{{x}^{2}-2xy+{y}^{2}}{xy}$•$\frac{x-y}{{x}^{2}}$
=x(y-x)×$\frac{xy}{(x-y)^{2}}$×$\frac{x-y}{{x}^{2}}$
=-1.
点评 此题主要考查了分式的乘除运算,正确将分子与分母因式分解是解题关键.

练习册系列答案
相关题目
15.下列说法不正确的是( )
| A. | 等腰三角形的两底角相等 | |
| B. | 等腰三角形的两条腰相等 | |
| C. | 两个内角分别为100°和40°的三角形是等腰三角形 | |
| D. | 等腰三角形的角平分线与高重合 |
 如图,在?ABCD中,AE:EB=1:2,且△AEF的面积为60cm2,求△CDF的面积.
如图,在?ABCD中,AE:EB=1:2,且△AEF的面积为60cm2,求△CDF的面积.
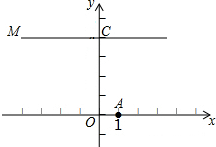 如图,在平面直角坐标系内,O为原点,点A的坐标为(1,0),点C的坐标为(0,4),直线CM⊥x轴,直线y=-x+b(b为常数)经过点A,且与直线CM相交于点D,连结OD.
如图,在平面直角坐标系内,O为原点,点A的坐标为(1,0),点C的坐标为(0,4),直线CM⊥x轴,直线y=-x+b(b为常数)经过点A,且与直线CM相交于点D,连结OD. 如图,∠ABC=∠DCB,再添加条件∠A=∠D或∠ACB=∠DCB 或条件AB=DC,就可以判定△ABC≌△DCB.
如图,∠ABC=∠DCB,再添加条件∠A=∠D或∠ACB=∠DCB 或条件AB=DC,就可以判定△ABC≌△DCB.