题目内容
19.若关于x的方程$\frac{1}{x-3}$+3=$\frac{m-x}{3-x}$有增根,则m的值是( )| A. | -2 | B. | 2 | C. | 1 | D. | -1 |
分析 解分式方程找出方程的根为x=4-$\frac{m}{2}$,由此根为增根可得出4-$\frac{m}{2}$=3,解之即可得出m的值.
解答 解:方程$\frac{1}{x-3}$+3=$\frac{m-x}{3-x}$可变形为1+3(x-3)=x-m,
解得:x=4-$\frac{m}{2}$.
∵原分式方程有增根,
∴4-$\frac{m}{2}$=3,
解得:m=2.
故选B.
点评 本题考查了分式方程的增根以及解分式方程,根据原分式方程有增根找出4-$\frac{m}{2}$=3是解题的关键.

练习册系列答案
相关题目
9.下列调查中,适宜采用全面调查方式的是( )
| A. | 调查乘坐飞机的旅客是否携带了违禁物品 | |
| B. | 调查2017年央视春晚的全国收视率 | |
| C. | 调查某品牌日光灯的使用寿命 | |
| D. | 调查市场上营养快线的质量 |
7.下列图形中不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
4.我县七年级今年有4500名学生参加本次考试,要想了解这4500名学生的数学成绩从中抽取了500名考生的数学成绩进行统计分析,以下说法正确的是( )
| A. | 这500名考生是总体的一个样本 | B. | 每位考生是个体 | ||
| C. | 500名考生是总体 | D. | 这种调查是抽样调查 |
8.把一张面值10元的人民币兑换成1元或2元的零钱,兑换方案有( )
| A. | 9种 | B. | 8种 | C. | 7种 | D. | 6种 |
9.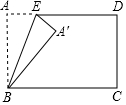 将一张长方形纸片ABCD沿BE折叠,得到如图所示的图形,若∠A′ED=40°,则∠A′BC的度数为( )
将一张长方形纸片ABCD沿BE折叠,得到如图所示的图形,若∠A′ED=40°,则∠A′BC的度数为( )
 将一张长方形纸片ABCD沿BE折叠,得到如图所示的图形,若∠A′ED=40°,则∠A′BC的度数为( )
将一张长方形纸片ABCD沿BE折叠,得到如图所示的图形,若∠A′ED=40°,则∠A′BC的度数为( )| A. | 35° | B. | 40° | C. | 50° | D. | 70° |
 如图,函数y=ax+4和y=bx的图象相交于点A,则不等式bx≥ax+4的解集为x≥2.
如图,函数y=ax+4和y=bx的图象相交于点A,则不等式bx≥ax+4的解集为x≥2.