题目内容
10.已知反比例函数的图象经过点A(3,-4).(1)这个函数的图象分布在哪些象限?在图象的每一支上,y随x的增大如何变化?
(2)点B(-3,4),点C(-2,6)和点D(3,4)是否在这个函数的图象上?
分析 (1)设函数关系式为y=$\frac{k}{x}$,把点A(3,-4)代入即可求出解析式,根据反比例函数的性质得出图象分布的象限;根据反比例函数的性质得出增减性;
(2)根据反比例函数的特点可得出k=-12,再判断点B(-3,4),点C(-2,6)和点D(3,4)是否在反比例函数的图象上.
解答 解:(1)设函数关系式为y=$\frac{k}{x}$,
∵反比例函数的图象过点A(3,-4),
∴k=3×(-4)=-12,
∵-12<0,
∴这个反比例函数图象分布在第二、四象限;在图象的每一支上,y随x的增大而增大;
(2)∵(-3)×4=-12,(-2)×6=-12,3×4=12,
∴点B(-3,4),点C(-2,6)在图象上,点D(3,4)不在图象上.
点评 本题考查了反比例函数图象上点的坐标特征,用待定系数法求反比例函数的解析式以及反比例函数的性质,是基础知识要熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列事件为必然事件的是( )
| A. | 王华期末考试数学成绩会是100分 | |
| B. | 某射击运动员射靶一次,正中靶心 | |
| C. | 打开电视机,CCTV第一套节目正在播放新闻 | |
| D. | 口袋中装有2个红球和一个白球,从中摸出2个球,其中必有红球 |
19.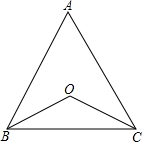 如图,点O在△ABC内,且到三边的距离相等.若∠BOC=120°,则tanA的值为( )
如图,点O在△ABC内,且到三边的距离相等.若∠BOC=120°,则tanA的值为( )
 如图,点O在△ABC内,且到三边的距离相等.若∠BOC=120°,则tanA的值为( )
如图,点O在△ABC内,且到三边的距离相等.若∠BOC=120°,则tanA的值为( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
13.(-3)2+(-2)3=( )
| A. | -12 | B. | -17 | C. | 1 | D. | 17 |
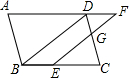 如图,在?ABCD中,点E在边BC上,点F在边AD的延长线上,且DF=BE,EF与CD交于点G.
如图,在?ABCD中,点E在边BC上,点F在边AD的延长线上,且DF=BE,EF与CD交于点G. 如图,矩形ABCD在第一象限,四边分别平行于x轴和y轴,且顶点A、C在反比例函数图象上,BA延长线交y轴于点E,BC延长线交x轴于点F,S△AOE=$\frac{1}{2}$.
如图,矩形ABCD在第一象限,四边分别平行于x轴和y轴,且顶点A、C在反比例函数图象上,BA延长线交y轴于点E,BC延长线交x轴于点F,S△AOE=$\frac{1}{2}$.