题目内容
15.已知一个矩形四个顶点都在反比例函数y=$\frac{1}{x}$上,且其中一个顶点横坐标为2,求这个矩形面积.分析 根据反比例函数图象上点的坐标特征可得一个顶点为(2,$\frac{1}{2}$),再根据矩形四个顶点都在反比例函数y=$\frac{1}{x}$上,利用对称性可得其它三个顶点为($\frac{1}{2}$,2),(-2,-$\frac{1}{2}$),(-$\frac{1}{2}$,-2),最后利用两点间距离公式即可得到矩形的边长以及面积.
解答 解:∵矩形顶点在反比例函数y=$\frac{1}{x}$上,且其中一个顶点横坐标为2,
∴当x=2时,y=$\frac{1}{2}$,即一个顶点为(2,$\frac{1}{2}$),
又∵矩形四个顶点中,相邻的顶点关于直线y=x或y=-x对称,
∴其它三个顶点为($\frac{1}{2}$,2),(-2,-$\frac{1}{2}$),(-$\frac{1}{2}$,-2),
∴矩形的边长为:$\sqrt{(-\frac{1}{2}-2)^{2}+(-2-\frac{1}{2})^{2}}$=$\frac{5}{2}\sqrt{2}$,$\sqrt{(2-\frac{1}{2})^{2}+(\frac{1}{2}-2)^{2}}$=$\frac{3}{2}\sqrt{2}$,
∴矩形的面积=$\frac{5}{2}\sqrt{2}$×$\frac{3}{2}\sqrt{2}$=$\frac{15}{2}$.
点评 本题主要考查了反比例函数图象上点的坐标特征以及反比例函数的图象的运用,解题时注意:图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
相关题目
6.某工厂接到加工600件衣服的订单,预计每天做25件,正好按时完成,后因客户要求提前3天交货,工人则需要提高每天的工作效率,设工人每天应多做x件,依题意列方程正确的是( )
| A. | $\frac{600}{25+x}$-$\frac{600}{25}$=3 | B. | $\frac{600}{25}$+3=$\frac{600}{x}$ | C. | $\frac{600}{25}$-$\frac{600}{x}$=3 | D. | $\frac{600}{25}$-$\frac{600}{25+x}$=3 |
3.线段EF是由线段PQ平移得到的,点P(-2,4)的对应点为E(3,0),则点Q(-3,-1)的对应点F的坐标为( )
| A. | (-8,3) | B. | (-8,-5) | C. | (2,-5) | D. | (2,3) |
10.关于x的一元二次方程x2+2x-m=0有实数根,则m的取值范围是( )
| A. | m≥-1 | B. | m>-1 | C. | m≤-1 | D. | m<-1 |
7.为了记录一个病人的体温变化情况,应选择的统计图是( )
| A. | 条形统计图 | B. | 扇形统计图 | C. | 折线统计图 | D. | 频数分布直方图 |
4.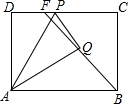 如图,矩形ABCD 中,AB=4,AD=3,P 是边CD 上一点,将△ADP沿直线AP对折,得到△APQ.当射线BQ交线段CD于点F时,DF的最大值是( )
如图,矩形ABCD 中,AB=4,AD=3,P 是边CD 上一点,将△ADP沿直线AP对折,得到△APQ.当射线BQ交线段CD于点F时,DF的最大值是( )
 如图,矩形ABCD 中,AB=4,AD=3,P 是边CD 上一点,将△ADP沿直线AP对折,得到△APQ.当射线BQ交线段CD于点F时,DF的最大值是( )
如图,矩形ABCD 中,AB=4,AD=3,P 是边CD 上一点,将△ADP沿直线AP对折,得到△APQ.当射线BQ交线段CD于点F时,DF的最大值是( )| A. | 3 | B. | 2 | C. | 4-$\sqrt{7}$ | D. | 4-$\sqrt{5}$ |
5.下列计算正确的是( )
| A. | a3•a3=a9 | B. | (a+b)2=a2+b2 | C. | a2÷a2=0 | D. | (a2)3=a6 |
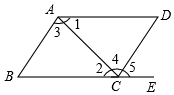 下列能判定AB∥CD的条件有( )个
下列能判定AB∥CD的条件有( )个