题目内容
6.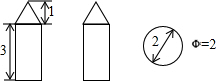 如图是某几何体的三视图及相关数据,则该几何体的表面积是( )
如图是某几何体的三视图及相关数据,则该几何体的表面积是( )| A. | 8π+$\sqrt{2}$π | B. | 7π+$\sqrt{2}$π | C. | 6π+$\sqrt{2}$π | D. | 7π2 |
分析 先根据几何体的三视图可得:该几何体由圆锥和圆柱组成,圆锥的底面直径=圆柱的底面直径=2,圆柱的高=3,然后根据圆锥的侧面积等于它展开后的扇形的面积,即S=$\frac{1}{2}$LR,扇形的弧长为底面圆的周长,扇形的半径为圆锥的母线长;圆柱侧面积等于展开后矩形的面积,矩形的长为圆柱的高,宽为底面圆的周长;而该几何体的表面积=圆锥的侧面积+圆柱的侧面积+圆柱的底面积.
解答 解:根据几何体的三视图可得:该几何体由圆锥和圆柱组成,圆锥的底面直径=2,圆锥的母线长为$\sqrt{2}$,
∴圆锥的侧面积=$\frac{1}{2}$•2π•1•$\sqrt{2}$=$\sqrt{2}$π,
圆柱的侧面积=2π•1•3=6π,
圆柱的底面积=π•12=π,
∴该几何体的表面积=7π+$\sqrt{2}$π.
故选B.
点评 本题考查了圆锥的侧面积的计算方法:圆锥的侧面积等于它展开后的扇形的面积,扇形的弧长为底面圆的周长,扇形的半径为圆锥的母线长;也考查了看三视图和求圆柱的侧面积的能力.

练习册系列答案
相关题目
17.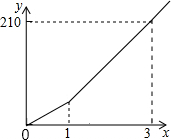 一辆汽车在行驶过程中,路程y(千米)与时间x(小时)之间的函数关系如图4所示,已知开始1小时的行驶速度是60千米/时,那么1小时以后的速度是( )
一辆汽车在行驶过程中,路程y(千米)与时间x(小时)之间的函数关系如图4所示,已知开始1小时的行驶速度是60千米/时,那么1小时以后的速度是( )
 一辆汽车在行驶过程中,路程y(千米)与时间x(小时)之间的函数关系如图4所示,已知开始1小时的行驶速度是60千米/时,那么1小时以后的速度是( )
一辆汽车在行驶过程中,路程y(千米)与时间x(小时)之间的函数关系如图4所示,已知开始1小时的行驶速度是60千米/时,那么1小时以后的速度是( )| A. | 70千米/时 | B. | 75千米/时 | C. | 105千米/时 | D. | 210千米/时 |
18.表2是从表1中截取的一部分,则a的值为( )


| A. | 11 | B. | 12 | C. | 16 | D. | 18 |
15. x、y、z在数轴上的位置如图所示,则化简|x-y|+|z-y|的结果是( )
x、y、z在数轴上的位置如图所示,则化简|x-y|+|z-y|的结果是( )
 x、y、z在数轴上的位置如图所示,则化简|x-y|+|z-y|的结果是( )
x、y、z在数轴上的位置如图所示,则化简|x-y|+|z-y|的结果是( )| A. | x+z-2y | B. | 2y-x-z | C. | z-x | D. | x-z |
16.如图,下面几何体的俯视图不是圆的是( )
| A. |  | B. |  | C. |  | D. |  |
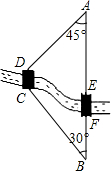 如图所示,A、B两地之间有一条河,原来从A地到B地需要经过桥DC,沿折线A→D→C→B到达,现在新建了桥EF(EF=DC),可直接沿直线AB从A地到达B地,已知BC=12km,∠A=45°,∠B=30°,桥DC和AB平行.
如图所示,A、B两地之间有一条河,原来从A地到B地需要经过桥DC,沿折线A→D→C→B到达,现在新建了桥EF(EF=DC),可直接沿直线AB从A地到达B地,已知BC=12km,∠A=45°,∠B=30°,桥DC和AB平行.