题目内容
2. 如图,在正五边形ABCDE中,以BC为一边,在形内作等边△BCF,连结AF.则∠AFB的大小是66度.
如图,在正五边形ABCDE中,以BC为一边,在形内作等边△BCF,连结AF.则∠AFB的大小是66度.
分析 根据等边三角形的性质得到BF=BC,∠FBC=60°,由正五边形的性质得到AB=BC,∠ABC=108°,等量代换得到AB=BF,∠ABF=48°,根据三角形的内角和即可得到结论.
解答 解:∵△BCF是等边三角形,
∴BF=BC,∠FBC=60°,
∵在正五边形ABCDE中,AB=BC,∠ABC=108°,
∴AB=BF,∠ABF=48°,
∴∠AFB=∠BAF=$\frac{180°-∠ABF}{2}$=66°,
故答案为:66.
点评 本题考查了正多边形的内角和,等边三角形的性质,等腰三角形的性质,熟记正多边形的内角的求法是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.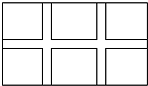 如图,学校课外生物小组的实验圆地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道.要使种植面积为600平方米,若设小道的宽为x米,则所列方程正确的是( )
如图,学校课外生物小组的实验圆地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道.要使种植面积为600平方米,若设小道的宽为x米,则所列方程正确的是( )
 如图,学校课外生物小组的实验圆地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道.要使种植面积为600平方米,若设小道的宽为x米,则所列方程正确的是( )
如图,学校课外生物小组的实验圆地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道.要使种植面积为600平方米,若设小道的宽为x米,则所列方程正确的是( )| A. | 35×20-2×20x-35x=600 | B. | 35×20-20x-35x+x2=600 | ||
| C. | (35-2x)(20-x)=600 | D. | (35-x)(20-x)=600 |
11.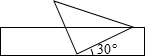 如图,将一个含有45°角的直角三角板的直角顶点放在一张宽为2cm的矩形纸带边沿上,另一个顶点在纸带的另一边沿上.若测得三角板的一边与纸带的一边所在的直线成30°角,则三角板最长边的长是( )
如图,将一个含有45°角的直角三角板的直角顶点放在一张宽为2cm的矩形纸带边沿上,另一个顶点在纸带的另一边沿上.若测得三角板的一边与纸带的一边所在的直线成30°角,则三角板最长边的长是( )
 如图,将一个含有45°角的直角三角板的直角顶点放在一张宽为2cm的矩形纸带边沿上,另一个顶点在纸带的另一边沿上.若测得三角板的一边与纸带的一边所在的直线成30°角,则三角板最长边的长是( )
如图,将一个含有45°角的直角三角板的直角顶点放在一张宽为2cm的矩形纸带边沿上,另一个顶点在纸带的另一边沿上.若测得三角板的一边与纸带的一边所在的直线成30°角,则三角板最长边的长是( )| A. | 2cm | B. | 4cm | C. | 2$\sqrt{2}$cm | D. | 4$\sqrt{2}$cm |
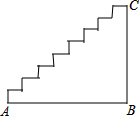 如图是小明家的楼梯示意图,其水平距离(即:AB的长度)为(2a+b)米,一只蚂蚁从A点沿着楼梯爬到C点,共爬了(3a-b)米.问小明家楼梯的竖直高点(即:BC的长度)为多少米.
如图是小明家的楼梯示意图,其水平距离(即:AB的长度)为(2a+b)米,一只蚂蚁从A点沿着楼梯爬到C点,共爬了(3a-b)米.问小明家楼梯的竖直高点(即:BC的长度)为多少米.
 如图所示,网格中有△ABC和点D,请你找出另外两点E、F,在图中画出△DEF,使△ABC≌△DEF,且顶点A、B、C分别与D、E、F对应.
如图所示,网格中有△ABC和点D,请你找出另外两点E、F,在图中画出△DEF,使△ABC≌△DEF,且顶点A、B、C分别与D、E、F对应.