题目内容
4.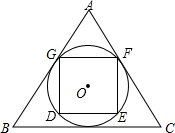 如图,正△ABC外切于⊙O,正方形DEFG内接于⊙O,若正△ABC的边长为6,求正方形的DEFG的边长.
如图,正△ABC外切于⊙O,正方形DEFG内接于⊙O,若正△ABC的边长为6,求正方形的DEFG的边长.
分析 设⊙O与BC相切于点M,连接OM、OB、OD、OE,则∠OMB=90°,∠OBM=30°,由正三角形的性质得出BM=$\frac{1}{2}$BC=3,求出OM=BM•tan30°=$\sqrt{3}$,得出OD=OE=$\sqrt{3}$,由正方形的性质得出△DOE是等腰直角三角形,得出DE=$\sqrt{2}$OD,即可得出结果.
解答 解:设⊙O与BC相切于点M,连接OM、OB、OD、OE,如图所示: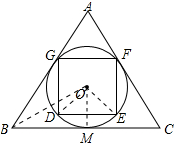
则∠OMB=90°,∠OBM=30°,
∴BM=$\frac{1}{2}$BC=3,
∴OM=BM•tan30°=$\sqrt{3}$,
∴OD=OE=$\sqrt{3}$,
∵四边形DEFG是正方形,
∴∠DOE=90°,
∴△DOE是等腰直角三角形,
∴DE=$\sqrt{2}$OD=$\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$,
即正方形的DEFG的边长为$\sqrt{6}$.
点评 本题考查了正方形的性质、正三角形的性质、正多边形与圆的关系;熟练掌握正三角形和正方形的性质,由题意求出正三角形内切圆的半径是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
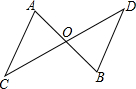 如图,点A,O,B在同一直线上,且△ACO≌△BDO.证明:
如图,点A,O,B在同一直线上,且△ACO≌△BDO.证明: 如图,已知△ABC中,CD是∠ACB的角平分线,EF垂直平分CD交AB延长线于点F,求证:DF2=AF•BF.
如图,已知△ABC中,CD是∠ACB的角平分线,EF垂直平分CD交AB延长线于点F,求证:DF2=AF•BF.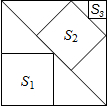 如图,边长为18的大正方形中有三个小正方形,若三个小正方形的面积分别为S1、S2、S3,则S1+S2+S3的值162.
如图,边长为18的大正方形中有三个小正方形,若三个小正方形的面积分别为S1、S2、S3,则S1+S2+S3的值162.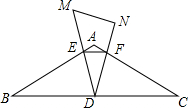 已知△ABC中,AB=AC=8,∠B=30°,D为BC上中点,Rt△DNM中,∠MDN=30°,D为定点,DM、DN交AB、AC于E、F.
已知△ABC中,AB=AC=8,∠B=30°,D为BC上中点,Rt△DNM中,∠MDN=30°,D为定点,DM、DN交AB、AC于E、F.