题目内容
17.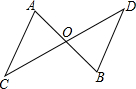 如图,点A,O,B在同一直线上,且△ACO≌△BDO.证明:
如图,点A,O,B在同一直线上,且△ACO≌△BDO.证明:(1)点C,O,D在同一直线上;
(2)AC∥BD.
分析 (1)由全等三角形的性质可知,由题意可知∠AOD+∠DOB=180°,故此可求得∠AOD+∠AOC=180°,从而可证明点C,O,D在同一直线上;
(2)由全等三角形的性质可知∠A=∠B,由平行线的判定定理可证明AC∥BD.
解答 解:(1)∵△ACO≌△BDO,
∴∠AOC=∠BOD.
∵点A,O,B在同一直线上,
∴∠AOD+∠DOB=180°.
∴∠AOD+∠AOC=180°.
∴点C,O,D在同一直线上.
(2)∵△ACO≌△BDO,
∴∠A=∠B.
∴AC∥BD.
点评 本题主要考查的是全等三角形的性质、平行线的判定,掌握全等三角形的性质、平行线的判定定理是解题的关键.

练习册系列答案
相关题目
7.多项式1-2xy+2xy3的次数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
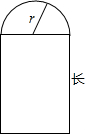 一个窗框的形状如图所示,已知窗框外围的周长为l,半圆的半径为r.
一个窗框的形状如图所示,已知窗框外围的周长为l,半圆的半径为r.
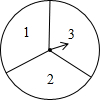 2015年1月9日,2014年度国家科学技术奖励大会在北京人民大会堂举行.为了加强青少年科技创新的意识,某市举办了科学表演大赛.小丽和小红想利用转转盘的游戏决定谁去参加该大赛,游戏规则如下:如图是一个可以自由转动的转盘,被平均分成3个扇形,扇形上分别标有数字1,2,3,转动一次转盘,任其自由停止,指针会指向某个扇形(若指针指在分界线上,则重转),相应地得到一个数字,两人各转动一次,若得到的两个数字之和为偶数,则小丽去参赛,否则小红去参赛.
2015年1月9日,2014年度国家科学技术奖励大会在北京人民大会堂举行.为了加强青少年科技创新的意识,某市举办了科学表演大赛.小丽和小红想利用转转盘的游戏决定谁去参加该大赛,游戏规则如下:如图是一个可以自由转动的转盘,被平均分成3个扇形,扇形上分别标有数字1,2,3,转动一次转盘,任其自由停止,指针会指向某个扇形(若指针指在分界线上,则重转),相应地得到一个数字,两人各转动一次,若得到的两个数字之和为偶数,则小丽去参赛,否则小红去参赛.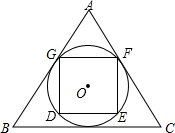 如图,正△ABC外切于⊙O,正方形DEFG内接于⊙O,若正△ABC的边长为6,求正方形的DEFG的边长.
如图,正△ABC外切于⊙O,正方形DEFG内接于⊙O,若正△ABC的边长为6,求正方形的DEFG的边长.