题目内容
如图,直线y=
x+m与抛物线y=-x2+bx+c交于C、D两点,其中点C在y轴上,点D的坐标为(3,
),点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
(1)求一次函数和抛物线的解析式;
(2)若点P的横坐标为t,当t为何值时,四边形OCPE是平行四边形?请说明理由;
(3)在CD上方是否存在点P,使∠PCF=45°?若存在,求出相应的点P的坐标;若不存在,试说明理由.

| 1 |
| 2 |
| 5 |
| 2 |
(1)求一次函数和抛物线的解析式;
(2)若点P的横坐标为t,当t为何值时,四边形OCPE是平行四边形?请说明理由;
(3)在CD上方是否存在点P,使∠PCF=45°?若存在,求出相应的点P的坐标;若不存在,试说明理由.

考点:二次函数综合题
专题:
分析:(1)首先求出点C的坐标,然后利用待定系数法求出抛物线的解析式;
(2)根据已知条件可知PE=OC=1,P点的纵坐标为1,把y=1代入抛物线的解析式,即可求出t的值;
(3)本问符合条件的点P有2个,如答图2所示,注意不要漏解.在求点P坐标的时候,需要充分挖掘已知条件,构造直角三角形或相似三角形,解方程求出点P的坐标
(2)根据已知条件可知PE=OC=1,P点的纵坐标为1,把y=1代入抛物线的解析式,即可求出t的值;
(3)本问符合条件的点P有2个,如答图2所示,注意不要漏解.在求点P坐标的时候,需要充分挖掘已知条件,构造直角三角形或相似三角形,解方程求出点P的坐标
解答:解:(1)∵直线y=
x+m经过点D(3,
),
∴
=
×3+m,解得:m=1,
∴直线的解析式:y=
x+1
在直线解析式y=
x+1中,令x=0,得y=1,
∴C(0,1).
∵点C(0,1)、D(3,
)在抛物线y=-x2+bx+c上,
∴c=1,
-9+3b+c=
,
解得b=
,c=1,
∴抛物线的解析式为y=-x2+
x+1;
(2)∵PF∥OC,且以O、C、P、F为顶点的四边形是平行四边形,
∴PF=OC=1,
设P(t,-t2+
t+1)则F(t,
t+1)
∴PF=|
t+1+t2-
t-1|=1,
解得:t=
或t=
.
(3)存在.
理由:设点P的横坐标为m,则P(m,-m2+
m+1),F(m,
m+1).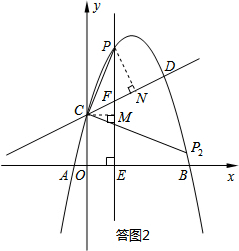
如答图2所示,过点C作CM⊥PE于点M,则CM=m,EM=1,
∴FM=yF-EM=
m,
∴tan∠CFM=2.
在Rt△CFM中,由勾股定理得:CF=
m.
过点P作PN⊥CD于点N,则PN=FN•tan∠PFN=FN•tan∠CFM=2FN.
∵∠PCF=45°,
∴PN=CN,
而PN=2FN,∴FN=CF=
m,PN=2FN=
m,
在Rt△PFN中,由勾股定理得:PF=
=
m.
∵PF=yP-yF=(-m2+
m+1)-(
m+1)=-m2+3m,
∴-m2+3m=
m,整理得:m2-
m=0,
解得m=0(舍去)或m=
,
∴P(
,
).
| 1 |
| 2 |
| 5 |
| 2 |
∴
| 5 |
| 2 |
| 1 |
| 2 |
∴直线的解析式:y=
| 1 |
| 2 |
在直线解析式y=
| 1 |
| 2 |
∴C(0,1).
∵点C(0,1)、D(3,
| 5 |
| 2 |
∴c=1,
-9+3b+c=
| 5 |
| 2 |
解得b=
| 7 |
| 2 |
∴抛物线的解析式为y=-x2+
| 7 |
| 2 |
(2)∵PF∥OC,且以O、C、P、F为顶点的四边形是平行四边形,
∴PF=OC=1,
设P(t,-t2+
| 7 |
| 2 |
| 1 |
| 2 |
∴PF=|
| 1 |
| 2 |
| 7 |
| 2 |
解得:t=
3+
| ||
| 2 |
3-
| ||
| 2 |
(3)存在.
理由:设点P的横坐标为m,则P(m,-m2+
| 7 |
| 2 |
| 1 |
| 2 |

如答图2所示,过点C作CM⊥PE于点M,则CM=m,EM=1,
∴FM=yF-EM=
| 1 |
| 2 |
∴tan∠CFM=2.
在Rt△CFM中,由勾股定理得:CF=
| ||
| 2 |
过点P作PN⊥CD于点N,则PN=FN•tan∠PFN=FN•tan∠CFM=2FN.
∵∠PCF=45°,
∴PN=CN,
而PN=2FN,∴FN=CF=
| ||
| 2 |
| 5 |
在Rt△PFN中,由勾股定理得:PF=
| FN2+PN2 |
| 5 |
| 2 |
∵PF=yP-yF=(-m2+
| 7 |
| 2 |
| 1 |
| 2 |
∴-m2+3m=
| 5 |
| 2 |
| 1 |
| 2 |
解得m=0(舍去)或m=
| 1 |
| 2 |
∴P(
| 1 |
| 2 |
| 5 |
| 2 |
点评:本题是二次函数综合题型,考查了二次函数的图象与性质、一次函数的图象与性质、解方程、平行四边形、勾股定理等重要知识点.第(2)问采用数形结合思想求解,直观形象且易于理解.

练习册系列答案
相关题目
下列命题中是假命题的是( )
| A、负数的平方根是负数 |
| B、平移不改变图形的形状和大小 |
| C、对顶角相等 |
| D、若a∥b,a⊥c,那么b⊥c |
下列多项式不能用公式法分解因式的是( )
| A、-x2+a2 | ||
| B、-x2+2x-1 | ||
C、x2-x+
| ||
| D、-a2-b2 |
 如图,在平面直角坐标系xOy中,直线x=2和直线y=ax交于点A,过A作AB⊥x轴于点B.如果a取1,2,3,…,n(n为正整数)时,对应的△AOB的面积为S1,S2,S3,…,Sn,那么S1=
如图,在平面直角坐标系xOy中,直线x=2和直线y=ax交于点A,过A作AB⊥x轴于点B.如果a取1,2,3,…,n(n为正整数)时,对应的△AOB的面积为S1,S2,S3,…,Sn,那么S1=