题目内容
7.阅读材料:如图1,在平面直角坐标系中,以坐标平面内任意一点M(a,b)为圆心,半径为r作圆,点P(x,y)在⊙M上,则必有(x-a)2+(y-b)2=r2.尝试证明:为了证明阅读材料上的结论,小明作了辅助线:过点M和点P分别作x轴、y轴的平行线,两平行线交于点N可得点N的坐标是(x,b)(用字母表示),完成小明的证明过程.
结论应用:如图2,点A、B、C均在坐标轴上,OB=OC=OA=4,过A、O、B作⊙D,E是⊙D上任意一点,连接CE,BE.
(1)当线段CE经过点D时,求点E的坐标;
(2)在点E的运动过程中,线段CE和线段BE的长度随之变化,试求CE2+BE2的最大值和最小值.
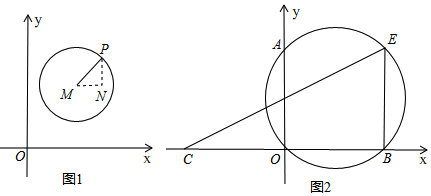
分析 尝试证明:直接点的坐标的特点即可得出结论;
结论应用:(1)先确定出⊙D的解析式,再确定出直线CE解析式,联立方程组即可得出点E坐标;
(2)设出点E坐标,进而表示出CE2+BE2,再根据极值确定出点E的坐标即可求出最大值和最小值.
解答 解:尝试证明:∵MN∥x轴,
∴点N的纵坐标和点M的纵坐标相同,是b,
∵PN∥y轴,
∴点N的横坐标和点P的横坐标相同,是x,
∴N(x,b);
故答案为(x,b).
结论应用:(1)如图,
∵点A、B、C均在坐标轴上,OB=OC=OA=4,
∴A(0,4),B(4,0),C(-4,0);
∴AB=4$\sqrt{2}$,
∵过A、O、B作⊙D,
∴D(2,2),
∴(x-2)2+(y-2)2=8①.
∵线段CE经过点D(2,2),C(-4,0),
∴直线CE解析式为y=$\frac{1}{3}$x+$\frac{4}{3}$②,
联立①②得,$\left\{\begin{array}{l}{x=2+\frac{6\sqrt{5}}{5}}\\{y=2+\frac{2\sqrt{5}}{5}}\end{array}\right.$或$\left\{\begin{array}{l}{x=2-\frac{6\sqrt{5}}{5}}\\{y=2-\frac{2\sqrt{5}}{5}}\end{array}\right.$(由于线段CE过点D,所以舍去),
∴E(2+$\frac{6\sqrt{5}}{5}$,2+$\frac{2\sqrt{5}}{5}$);
(2)设点E的坐标为(m,n)
,∵点E在⊙D上,
∴(m-2)2+(n-2)2=8,
∴m2+n2=4(m+n)③,
∵B(4,0),C(-4,0),
∴CE2+BE2=(m+4)2+n2+(m-4)2+n2=2(m2+n2)+32
∴m2+n2是表示⊙D上的任意一个点E到原点的距离,
∴当点E(0,0)时,CE2+BE2最小值为32,
当点E是射线OD和⊙D的交点时,
∵D(2,2),∴直线OD解析式为y=x,
∴m=n,将m=n代入③得,m=n=4,
∴CE2+BE2最大值为96.
点评 此题是圆的综合题,主要考查了圆的性质,待定系数法,平面坐标系内,两点间的距离公式,解方程组,极值确定,求出点E坐标是解本题的关键,确定出CE2+BE2的极值是解本题的难点.

 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案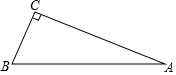 如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,则∠A的正弦值为( )
如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,则∠A的正弦值为( )| A. | $\frac{5}{12}$ | B. | $\frac{12}{13}$ | C. | $\frac{12}{5}$ | D. | $\frac{5}{13}$ |
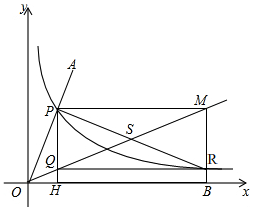 如图,在平面直角坐标系中,射线OA交反比例函数y=$\frac{1}{x}$(x>0)图象于点P,点R为反比例函数y=$\frac{1}{x}$(x>0)图象上的另一点,且PR=2OP,分别过点P、R作x轴、y轴的平行线,两线相交于点M(a,b),直线MR交x轴于点B,过点P作y轴的平行线分别交直线OM和x轴于点Q、H,连接RQ.
如图,在平面直角坐标系中,射线OA交反比例函数y=$\frac{1}{x}$(x>0)图象于点P,点R为反比例函数y=$\frac{1}{x}$(x>0)图象上的另一点,且PR=2OP,分别过点P、R作x轴、y轴的平行线,两线相交于点M(a,b),直线MR交x轴于点B,过点P作y轴的平行线分别交直线OM和x轴于点Q、H,连接RQ.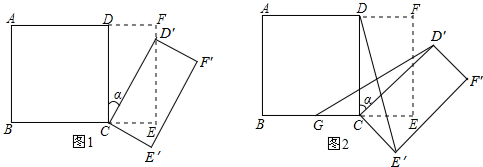
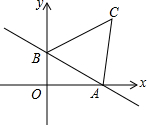 一次函数y=-$\frac{{\sqrt{3}}}{3}$x+1的图象与x轴、y轴分别交于点A、B,以AB为边在第一象限内做等边△ABC
一次函数y=-$\frac{{\sqrt{3}}}{3}$x+1的图象与x轴、y轴分别交于点A、B,以AB为边在第一象限内做等边△ABC