题目内容
18.在三角形ABC中,设∠A=xo,∠B=yo,且x,y满足方程组$\left\{\begin{array}{l}{2x+y=29n-1086}\\{3x-y=121n-4932}\end{array}\right.$(n是整数),则三角形ABC是锐角三角形吗?请说明理由.分析 把n看做已知数表示出方程组的解,求出n的范围,确定出n的值,判断三角形形状即可.
解答 解:三角形ABC不是锐角三角形解方程组$\left\{\begin{array}{l}2x+y=29n-1068\\ 3x-y=121n-4932.\end{array}$,得 $\left\{\begin{array}{l}x=30n-1200\\ y=-31n+1332.\end{array}$(n是整数),
由题意得$\left\{\begin{array}{l}30n-1200>0\\-31n+1332>0\end{array}$(n是整数),
解得:40<n<42$\frac{31}{32}$(n是整数),
当n=41时,∠A=30°,∠B=61°,
∴∠C=89°,此时三角形ABC是锐角三角形;
当n=42时,∠A=60°,∠B=30°,
∴∠C=90°,
此时三角形ABC是直角三角形,不是锐角三角形.
点评 此题考查了解二元一次方程组,以及三角形内角和定理,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
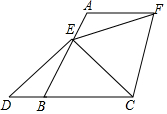 如图,已知△ABC是等边三角形,点E在线段AB上,点D在射线CB上,且ED=EC,以CE为边作等边△CEF,连接EF.
如图,已知△ABC是等边三角形,点E在线段AB上,点D在射线CB上,且ED=EC,以CE为边作等边△CEF,连接EF.
