题目内容
已知∠AOB内部有三条射线,其中OE平分∠BOC,OF平分∠AOC.
(1)如图1,若∠AOB=90°,∠AOC=30°,求EOF的度数;
(2)如图2,若∠AOB=α,求∠EOF的度数(用含α的式子表示);
(3)若将题中的“OE平分∠BOC,OF平分∠AOC”的条件改为“∠EOB=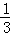 ∠BOC,∠COF=
∠BOC,∠COF= ∠AOC”,且∠AOB=α,求∠EOF的度数(用含α的式子表示)
∠AOC”,且∠AOB=α,求∠EOF的度数(用含α的式子表示)

【考点】角的计算;角平分线的定义.
【分析】(1)首先求得∠BOC的度数,然后根据角的平分线的定义和角的和差可得∠EOF=∠EOC+∠COF即可求解;
(2)根据角的平分线的定义和角的和差可得∠EOF=∠EOC+∠COF= ∠BOC+
∠BOC+ ∠AOC=
∠AOC= (∠BOC+∠AOC),即可求解;
(∠BOC+∠AOC),即可求解;
(3)根据角的等分线的定义可得∠EOF=∠EOC+∠COF= ∠BOC+
∠BOC+ ∠AOC=
∠AOC= (∠BOC+∠AOC)=
(∠BOC+∠AOC)= ∠AOB,即可求解.
∠AOB,即可求解.
【解答】解:(1)∠BOC=∠AOB﹣∠AOC=90°﹣30°=60°,
∵OE平分∠BOC,OF平分∠AOC,
∴∠EOC= ∠BOC=
∠BOC= ×60°=30°,∠COF=
×60°=30°,∠COF= ∠AOC=
∠AOC= ×30°=15°,
×30°=15°,
∴∠EOF=∠EOC+∠COF=30°+15°=45°;
(2)∵OE平分∠BOC,OF平分∠AOC,
∴∠EOC= ∠BOC,∠COF=
∠BOC,∠COF= ∠AOC,
∠AOC,
∴∠EOF=∠EOC+∠COF= ∠BOC+
∠BOC+ ∠AOC=
∠AOC= (∠BOC+∠AOC)=
(∠BOC+∠AOC)= ∠AOB=
∠AOB= a;
a;
(3)∵∠EOB=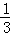 ∠BOC,
∠BOC,
∴∠EOC= ∠BOC,
∠BOC,
又∵∠COF= ∠AOC,
∠AOC,
∴∠EOF=∠EOC+∠COF= ∠BOC+
∠BOC+ ∠AOC=
∠AOC= (∠BOC+∠AOC)=
(∠BOC+∠AOC)= ∠AOB=
∠AOB= a.
a.
【点评】本题考查了角度的计算,理解角的平分线的定义以及角度的和、差之间的关系是关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目


 的值是 .
的值是 . B.
B. C.
C. D.
D.
 的数与
的数与 的和等于( )
的和等于( ) B.
B. C.
C. 或
或 D.
D. 或
或
 x+7是关于x的二次三项式,则m= .
x+7是关于x的二次三项式,则m= .