题目内容
15.方程2x2+(m2-1)x+m=0是关于x的方程,当m为何值时,方程的两根互为相反数?并求出这时方程的解.分析 根据方程两根互为相反数知两根和为0,可得关于m的方程,解方程求得m的值,并检验方程是否有两根可得.
解答 解:∵方程2x2+(m2-1)x+m=0的两根互为相反数,
∴$\frac{{m}^{2}-1}{2}$=0,解得:m=-1或m=1,
当m=-1时,方程为2x2-1=0,两根为x=$\frac{\sqrt{2}}{2}$或x=-$\frac{\sqrt{2}}{2}$;
当m=1时,方程为2x2+1=0,方程无解.
点评 本题主要考查方程的根与系数的关系,根据题意知两根和为0得关于m的方程是关键,要注意检验方程是否有两根.

练习册系列答案
相关题目
6. 如图,一个半径是2cm的圆,在其中画一个圆心角为120°的扇形,这个扇形的面积为( )cm2.
如图,一个半径是2cm的圆,在其中画一个圆心角为120°的扇形,这个扇形的面积为( )cm2.
 如图,一个半径是2cm的圆,在其中画一个圆心角为120°的扇形,这个扇形的面积为( )cm2.
如图,一个半径是2cm的圆,在其中画一个圆心角为120°的扇形,这个扇形的面积为( )cm2.| A. | $\frac{1}{3}$π | B. | $\frac{2}{3}$π | C. | π | D. | $\frac{4}{3}$π |
20. 下列图形中,如图所示几何体的俯视图的是( )
下列图形中,如图所示几何体的俯视图的是( )
 下列图形中,如图所示几何体的俯视图的是( )
下列图形中,如图所示几何体的俯视图的是( )| A. |  | B. |  | C. |  | D. |  |
 如图,已知AF∥CD,∠BAF=∠EDC,∠ABC=∠DEF,探索BC与EF的位置关系,并说明理由.
如图,已知AF∥CD,∠BAF=∠EDC,∠ABC=∠DEF,探索BC与EF的位置关系,并说明理由. 如果,如果AB∥CD,试猜想α、β、γ之间的关系,并说明理由.
如果,如果AB∥CD,试猜想α、β、γ之间的关系,并说明理由.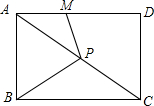 如图,点P为矩形ABCD的对角线AC上一点,PM⊥PB交AD于M.
如图,点P为矩形ABCD的对角线AC上一点,PM⊥PB交AD于M.