题目内容
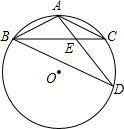如图，A、B、C、D是圆O上的四个点，AB=AC，AD交BC于点E，AE=3，AD=7，则AB的长为（ ）| A、3 | ||
B、2
| ||
C、
| ||
D、3
|
考点：圆周角定理,相似三角形的判定与性质
专题：计算题
分析：由AB=AC得到
=
，根据圆周角定理得到∠ABC=∠D，则可证明△ABE∽△ADB，然后利用相似比即可计算出AB的长．
 |
| AB |
|
| AC |
解答：解：∵AB=AC，
∴
=
，
∴∠ABC=∠D，
而∠BAE=∠DAB，
∴△ABE∽△ADB，
∴AB：AE=AD：AB，即AB：3=7：AB，
∴AB=
．
故选C．
∴
|
| AB |
|
| AC |
∴∠ABC=∠D，
而∠BAE=∠DAB，
∴△ABE∽△ADB，
∴AB：AE=AD：AB，即AB：3=7：AB，
∴AB=
| 21 |
故选C．
点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了相似三角形的判定与性质．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
如图为二次函数y=ax2+bx+c的图象，在下列说法中：
如图所示，AB是⊙O的一条弦，OD⊥AB，垂足为C，交⊙O于点D，点E在⊙O上．
如图是一个表面带有图案的正方体，则其表面展开图可能是（ ）A、 |
B、 |
C、 |
D、 |
如图，AD∥BC，DC⊥AD，AE平分∠BAD，且点E是DC的中点．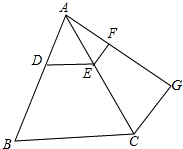
如图，DE∥BC，EF∥CG，AD：AB=1：3，AE=3．
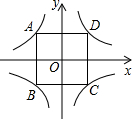在同一平面直角坐标系中，反比例函数y=
在正方形方格中，△ABC的顶点A、B、C在单位正方形的顶点上，请在图中画一个格点△A1B1C1使△A1B1C1∽△ABC（相似比不为1），且点都在单位正方形的顶点上．