题目内容
分解因式:(x2+4x)2-(x2+4x)-20= .
考点:因式分解-十字相乘法等,因式分解-运用公式法
专题:
分析:原式利用十字相乘法分解即可.
解答:解:原式=(x2+4x-5)(x2+4x+4)
=(x+2)2(x+5)(x-1).
故答案为:(x+2)2(x+5)(x-1).
=(x+2)2(x+5)(x-1).
故答案为:(x+2)2(x+5)(x-1).
点评:此题考查了因式分解-十字相乘法,熟练掌握十字相乘的方法是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
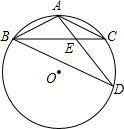 如图,A、B、C、D是圆O上的四个点,AB=AC,AD交BC于点E,AE=3,AD=7,则AB的长为( )
如图,A、B、C、D是圆O上的四个点,AB=AC,AD交BC于点E,AE=3,AD=7,则AB的长为( )| A、3 | ||
B、2
| ||
C、
| ||
D、3
|
多项式9a2x2-18a3x3-36a4x4各项的公因式是( )
| A、a2x2 |
| B、a3x3 |
| C、9a2x2 |
| D、9a4x4 |
下列单项式中,次数为5的是( )
| A、3x5y2 |
| B、-2x3y2 |
| C、-22x2y |
| D、4x5y |
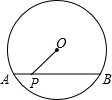 如图,⊙O的直径为10,弦AB的长是8,P是AB上的一个动点,则
如图,⊙O的直径为10,弦AB的长是8,P是AB上的一个动点,则