题目内容
 如图,四边形ABCD是菱形,AC、BD交于点O,DH⊥AB于H,连OH,若AC=8,OH=3,则AH=
如图,四边形ABCD是菱形,AC、BD交于点O,DH⊥AB于H,连OH,若AC=8,OH=3,则AH=考点:菱形的性质,直角三角形斜边上的中线,勾股定理
专题:
分析:根据菱形的对角线互相平分可得OD=OB,再根据直角三角形斜边上的中线等于斜边的一半可得OH=OB,所以BD可求,进而可求出菱形的面积,利用勾股定理可求出AB的长,由菱形的面积可求出DH的长,再利用勾股定理可求出AH的长.
解答:解:∵四边形ABCD是菱形,
∴OD=OB,∠COD=90°,
∵DH⊥AB,
∴OH=
BD=OB,
∴BD=6,
∴BO=3,S菱形ABCD=
×6×8=24,
∵AO=
AC=4,
∴AB=5,
∴DH=
,
∵AD=5,
∴AH=
=
,
故答案为:
.
∴OD=OB,∠COD=90°,
∵DH⊥AB,
∴OH=
| 1 |
| 2 |
∴BD=6,
∴BO=3,S菱形ABCD=
| 1 |
| 2 |
∵AO=
| 1 |
| 2 |
∴AB=5,
∴DH=
| 24 |
| 5 |
∵AD=5,
∴AH=
| AD2-DH2 |
| 7 |
| 5 |
故答案为:
| 7 |
| 5 |
点评:本题考查了菱形的对角线互相垂直平分的性质,直角三角形斜边上的中线等于斜边的一半的性质,勾股定理的运用,熟记各性质并理清图中边的关系是解题的关键.

练习册系列答案
相关题目
发射一枚炮弹,经过x秒后炮弹的高度为y米,x,y满足y=ax2+bx,其中a,b是常数,且a≠0.若此炮弹在第6秒与第14秒时的高度相等,则炮弹达到最大高度的时刻是( )
| A、第8秒 | B、第10秒 |
| C、第12秒 | D、第15秒 |
如图,用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究并观察,在第n个图中,共有瓷砖( )块.


| A、n2+n+6 |
| B、n2+4n+6 |
| C、n2+5n+6 |
| D、n2+5n+5 |
 如图,数轴上的点A所表示的数为a,化简|a|+|1-a|的结果为( )
如图,数轴上的点A所表示的数为a,化简|a|+|1-a|的结果为( )| A、1 | B、2a+1 |
| C、2a-1 | D、1-2a |
 如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=3,BC=4,CD=5.点E为线段CD上一动点(不与点C重合),△BCE关于BE的轴对称图形为△BFE,连接CF.设CE=x,△BCF的面积为S1,△CEF的面积为S2.
如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=3,BC=4,CD=5.点E为线段CD上一动点(不与点C重合),△BCE关于BE的轴对称图形为△BFE,连接CF.设CE=x,△BCF的面积为S1,△CEF的面积为S2.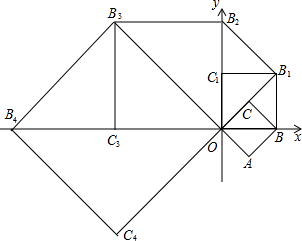 如图,在平面直角坐标系xOy中,有一边长为1的正方形OABC,点B在x轴的正半轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则B2的坐标是
如图,在平面直角坐标系xOy中,有一边长为1的正方形OABC,点B在x轴的正半轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则B2的坐标是