题目内容
8.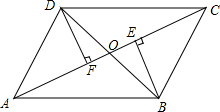 如图,四边形ABCD的对角线AC、BD相交于点O,BE⊥AC于点E,DF⊥AC于点F,点O既是AC的中点,又是EF的中点.
如图,四边形ABCD的对角线AC、BD相交于点O,BE⊥AC于点E,DF⊥AC于点F,点O既是AC的中点,又是EF的中点.(1)求证:△BOE≌△DOF;
(2)填空:
①连接BF、DE,则四边形BEDF是平行四边形.
②当BD=2OA时,四边形ABCD是矩形.
分析 (1)由垂直的定义得出∠OEB=∠OFD=90°,由中点的定义得出OE=OF,由ASA证明△BOE≌△DOF即可;
(2)①由全等三角形的性质得出OB=OD,由OE=OF,即可得出四边形BEDF是平行四边形;
②先证明四边形ABCD是平行四边形,再证出AC=BD,即可得出四边形ABCD是矩形.
解答 (1)证明:∵BE⊥AC,DF⊥AC,
∴∠OEB=∠OFD=90°,
∵O是EF的中点,
∴OE=OF,
在△BOE和△DOF中,
$\left\{\begin{array}{l}{∠OEB=∠OFD}&{\;}\\{OE=OF}&{\;}\\{∠BOE=∠DOF}&{\;}\end{array}\right.$,
∴△BOE≌△DOF(ASA);
(2)解:①四边形BEDF是平行四边形;理由如下:
∵△BOE≌△DOF,
∴OB=OD,
又∵OE=OF,
∴四边形BEDF是平行四边形;
故答案为:平行四边形;
②当BD=2OA时,四边形ABCD是矩形;理由如下:
∵O是AC的中点,
∴OA=OC=$\frac{1}{2}$AC,
又∵OB=OD,
∴四边形ABCD是平行四边形,
∵BD=2OA,
∴AC=BD,
∴四边形ABCD是矩形;
故答案为:2.
点评 本题考查了全等三角形的判定与性质、矩形的判定方法、平行四边形的判定;熟练掌握平行四边形的判定方法,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
19.下列方程:$xy+1=1,\sqrt{{x^2}-1}=2,\frac{1}{t}+{t^2}=1$,x(x+1)=x(x-2)+5,ax2+bx+cx2=0,x2-y+1=0,其中是一元二次方程的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
13.二元一次方程组$\left\{\begin{array}{l}{x+2y=1}\\{x-y=-2}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$ |
20.菱形ABCD的周长为16,∠A=60°,则BD的长为( )
| A. | 8 | B. | 4 | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
 长方体的主视图与左视图如图所示(单位:cm),则其俯视图的面积是12(cm2).
长方体的主视图与左视图如图所示(单位:cm),则其俯视图的面积是12(cm2).