题目内容
8.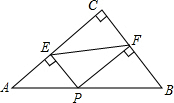 如图所示,在Rt△ABC中,∠C=90°,AC=4,BC=3,P为AB上一动点(不与A、B重合),作PE⊥AC于点E,PF⊥BC于点F,连接EF,则EF的最小值是2.4.
如图所示,在Rt△ABC中,∠C=90°,AC=4,BC=3,P为AB上一动点(不与A、B重合),作PE⊥AC于点E,PF⊥BC于点F,连接EF,则EF的最小值是2.4.
分析 连接CP,利用勾股定理列式求出AB,判断出四边形CFPE是矩形,根据矩形的对角线相等可得EF=CP,再根据垂线段最短可得CP⊥AB时,线段EF的值最小,然后根据三角形的面积公式列出方程求解即可.
解答 解:如图,连接CP.
∵∠C=90°,AC=3,BC=4,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵PE⊥AC,PF⊥BC,∠C=90°,
∴四边形CFPE是矩形,
∴EF=CP,
由垂线段最短可得CP⊥AB时,线段EF的值最小,
此时,S△ABC=$\frac{1}{2}$BC•AC=$\frac{1}{2}$AB•CP,
即$\frac{1}{2}$×4×3=$\frac{1}{2}$×5•CP,
解得CP=2.4.
故答案为:2.4.
点评 本题考查了矩形的判定与性质,垂线段最短的性质,勾股定理,判断出CP⊥AB时,线段EF的值最小是解题的关键,难点在于利用三角形的面积列出方程.

练习册系列答案
相关题目
3.方程组$\left\{\begin{array}{l}{y=2x-5}\\{3x-2y=8}\end{array}\right.$用代入法消去y后所得的方程是( )
| A. | 3x-4x-10=8 | B. | 3x-4x+5=8 | C. | 3x-4x-5=8 | D. | 3x-4x+10=8 |
13.中国的陆地面积约为9600000km.将9600000用科学记数法表示应为( )
| A. | 96×106 | B. | 96×105 | C. | 9.6×107 | D. | 9.6×106 |
17.2014年成都市的国民生产总值为1034亿元,1034亿元用科学记数法表示正确的是( )
| A. | 1034×108元 | B. | 1.034×1011元 | C. | 1.0×1011元 | D. | 1.034×1012元 |
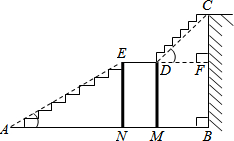 如图是某宾馆大厅到二楼的楼梯设计图,已知BC=5米,AB=8米,DM、EN为平台的两根支柱,DM、EN垂直于AB,垂足分别为M、N,∠EAB=30°,∠CDF=45°.
如图是某宾馆大厅到二楼的楼梯设计图,已知BC=5米,AB=8米,DM、EN为平台的两根支柱,DM、EN垂直于AB,垂足分别为M、N,∠EAB=30°,∠CDF=45°.