题目内容
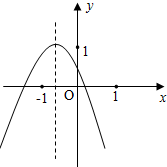 如图所示的是二次函数y=ax2+bx+c的图象,某学霸从下面五条信息中:
如图所示的是二次函数y=ax2+bx+c的图象,某学霸从下面五条信息中:(1)a<0;(2)b2-4ac>0;(3)c>1;(4)2a-b>0;(5)a+b+c<0.准确找到了其中错误的信息,它们分别是
考点:二次函数图象与系数的关系
专题:
分析:由抛物线的开口方向判断a与0的关系;根据抛物线与x轴交点个数判断b2-4ac与0的关系;由抛物线与y轴的交点判断c与1的关系;根据对称轴在x=-1的左边判断2a-b与0的关系;把x=1,y=0代入y=ax2+bx+c,可判断a+b+c<0是否成立.
解答:解:(1)∵抛物线的开口向下,
∴a<0,故本信息正确;
(2)根据图示知,该函数图象与x轴有两个交点,
故△=b2-4ac>0;
故本信息正确;
(3)由图象知,该函数图象与y轴的交点在点(0,1)以下,
所以c<1,故本信息错误;
(4)由图示,知对称轴x=-
>-1;
又∵a<0,
∴-b<-2a,即2a-b<0,故本信息错误;
(5)根据图示可知,当x=1,即y=a+b+c<0,
所以a+b+c<0,故本信息正确;
故答案为(1)(2)(5).
∴a<0,故本信息正确;
(2)根据图示知,该函数图象与x轴有两个交点,
故△=b2-4ac>0;
故本信息正确;
(3)由图象知,该函数图象与y轴的交点在点(0,1)以下,
所以c<1,故本信息错误;
(4)由图示,知对称轴x=-
| b |
| 2a |
又∵a<0,
∴-b<-2a,即2a-b<0,故本信息错误;
(5)根据图示可知,当x=1,即y=a+b+c<0,
所以a+b+c<0,故本信息正确;
故答案为(1)(2)(5).
点评:主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
相关题目
下列各组中的两项是同类项的是( )
| A、ab和abc |
| B、a和a3 |
| C、5x2y和-2xy2 |
| D、-3xy和3yx |
下列各数:-3.8,+5,0,-
,-(8),
,-4,-|-1|,其中属于负数的个数为( )
| 1 |
| 2 |
| 3 |
| 5 |
| A、3 | B、4 | C、5 | D、6 |
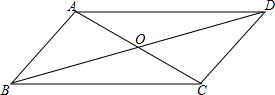 已知?ABCD的周长为68cm,对角线交于点O,△ABO与△ADO的周长和等于80cm,两对角线的长度之比是2:3,求两条对角线的长度.
已知?ABCD的周长为68cm,对角线交于点O,△ABO与△ADO的周长和等于80cm,两对角线的长度之比是2:3,求两条对角线的长度. 如图,矩形OABC和?ABEF,B(3,4).
如图,矩形OABC和?ABEF,B(3,4).