Question

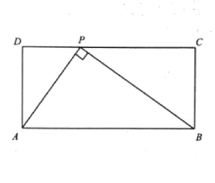
【题目】已知:在矩形中，，分别是边，上的点，过点作的垂线交于点，以为直径作半圆．

（1）填空：点_____________（填“在”或“不在”）上；当时，的值是_____________；

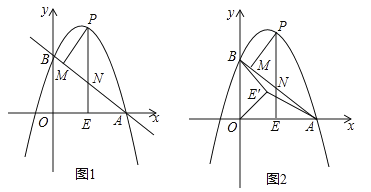
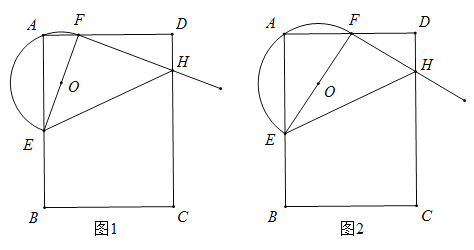
（2）如图1，在中，当时，求证：；

（3）如图2，当的顶点是边的中点时，请直接写出三条线段的数量关系．

Answer 1

【答案】（1）在，1；（2）证明见解析；（3）

【解析】

（1）连接OA，,O为EF中点，所以，因此点A在，根据分析可得，即可求得结果．　

（2）证明，得到AF=DH，AE=DFA,所以AD=AF+DF=AE+DH．

（3）延长EF交DH的延长线于点G，先证明，所以AC=DG，EF=FG，因为，所以EH=GH，GH=DH+DG=DH+AE，即EH=AE+DH．

解：（1）在，1；

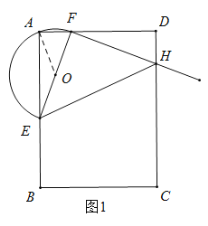
连接OA，

∵，O为EF的中点，

所以，

所以A在，

当弧AE=弧AF时，,

所以．

（2），，

在矩形中，，

，，

，

又，，

，，

；

（3）延长EF交HD的延长线于点G，

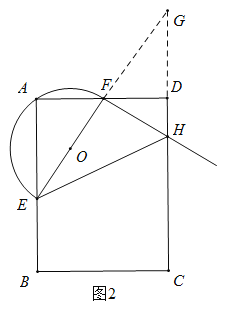
∵F是AD上的中点，

∴AF=DF，

∵，，

∴，

∴AE=DG，EF=FG，

∵，

∴EH=GH，

∴GH=DH+DG=DH+AE，

；