Question

【题目】如图1，抛物线与轴交于点，与轴交于点，在轴上有一动点，过点作轴的垂线交直线于点，交抛物线于点，过点作于点．

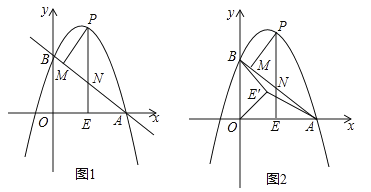
（1）求的值和直线的函数表达式；

（2）设的周长为，的周长为，若，求的值；

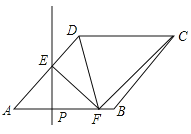
（3）如图2，在（2）条件下，将线段绕点逆时针旋转得到，旋转角为，连接、，求的最小值．

Answer 1

【答案】（1），；（2）；（3）

【解析】

（1）令y=0，求出抛物线与x轴交点，列出方程即可求出a，根据待定系数法可以确定直线AB解析式；

（2）由△PNM∽△ANE，推出，列出方程即可解决问题．
（3）在y轴上 取一点M使得OM′=，构造相似三角形，可以证明AM′就是的最小值．

解：（1）令，则，

，

或，

抛物线与轴交于点，

，

．

，，

设直线解析式为，则，

解得，

直线解析式为；

（2）如图1中，

，，

，

，

，

，

，

，

，

抛物线解析式为，

，

，

解得；

（3）如图2中，在轴上 取一点使得，连接，在上取一点使得．

，，

，

，

，

△△，

，

，

，

此时最小（两点间线段最短，、、共线时），

最小值．