题目内容
10．二次函数y=ax2-2ax+3的图象与x轴有两个交点，其中一个交点坐标为（-1，0），则一元二次方程ax2-2ax+3=0的解为x1=-1，x2=3．分析 根据题意把x=-1代入ax2-2ax+3=0求出a，得到关于x的一元二次方程，解方程得到答案．
解答 解：根据题意，x=-1是ax2-2ax+3=0的根，
∴a=-1，
一元二次方程-x2+2x+3=0的解为：x1=-1，x2=3，
故答案为：x1=-1，x2=3．
点评 本题考查的是抛物线与x轴的交点问题，掌握二次函数与一元二次方程的关系是解题的关键，方程ax2+bx+c=0的两根就是抛物线y=ax2+bx+c与x轴交点的横坐标．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
1．关于x的一元二次方程（m-1）x2-2mx+m+1=0（ ）
| A． | 方程有两个不相等的实数根 | B． | 方程有两个相等的实数根 | ||
| C． | 方程无实数根 | D． | 方程的实数根与m有关 |
18．$\sqrt{3}$的相反数是（ ）
| A． | $\sqrt{3}$ | B． | $\frac{{\sqrt{3}}}{3}$ | C． | -$\sqrt{3}$ | D． | -$\frac{\sqrt{3}}{3}$ |
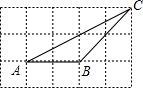如图，每个小正方形的边长为1，△ABC的顶点都在方格纸的格点上，则sinA=$\frac{\sqrt{5}}{5}$．
4．平面直角坐标系中，在第四象限的点是（ ）
| A． | （1，2） | B． | （1，-2） | C． | （-1，2） | D． | （-1，-2） |
