题目内容
3.化简$\frac{{{a^2}-1}}{{{a^2}+2a+1}}÷\frac{a-1}{a}$的结果是( )| A. | $\frac{1}{2}$ | B. | $\frac{a}{a+1}$ | C. | $\frac{a+1}{a}$ | D. | $\frac{a+1}{a+2}$ |
分析 首先将能分解因式的进行分解因式,进而化简求出即可.
解答 解:原式=$\frac{(a-1)(a+1)}{(a+1)^{2}}$×$\frac{a}{a-1}$
=$\frac{a}{a+1}$.
故选:B.
点评 此题主要考查了分式的乘除法,正确分解因式得出是解题关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
13.在以下四个标志中,轴对称图形是( )
| A. |  | B. |  | C. |  | D. |  |
14. 如图,直径为10的⊙A经过点C(0,5)和点O (0,0),B是y轴右侧⊙A优弧上一点,则tan∠OBC的值为( )
如图,直径为10的⊙A经过点C(0,5)和点O (0,0),B是y轴右侧⊙A优弧上一点,则tan∠OBC的值为( )
 如图,直径为10的⊙A经过点C(0,5)和点O (0,0),B是y轴右侧⊙A优弧上一点,则tan∠OBC的值为( )
如图,直径为10的⊙A经过点C(0,5)和点O (0,0),B是y轴右侧⊙A优弧上一点,则tan∠OBC的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\sqrt{3}$ |
11.某中学为了解学生的视力情况,需要抽取部分学生进行调查,下列抽取方法中最合适的是( )
| A. | 随机抽取一部分男生 | |
| B. | 随机抽取一个班级的学生 | |
| C. | 随机抽取一个年级的学生 | |
| D. | 在各个年级中,每班各随机抽取20名学生 |
18.$\sqrt{3}$的相反数是( )
| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | -$\sqrt{3}$ | D. | -$\frac{\sqrt{3}}{3}$ |
8.|-3|的相反数是( )
| A. | -3 | B. | 3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
12. 如图,在⊙O中,∠AOB=45°,则∠C为( )
如图,在⊙O中,∠AOB=45°,则∠C为( )
 如图,在⊙O中,∠AOB=45°,则∠C为( )
如图,在⊙O中,∠AOB=45°,则∠C为( )| A. | 22.5° | B. | 45° | C. | 60° | D. | 90° |
18.若M(m,1-2m)是第四象限上的点,则m的取值范围是( )
| A. | x>0 | B. | m>$\frac{1}{2}$ | C. | 0$<m<\frac{1}{2}$ | D. | -$\frac{1}{2}$<m<0 |
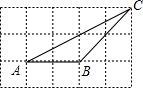 如图,每个小正方形的边长为1,△ABC的顶点都在方格纸的格点上,则sinA=$\frac{\sqrt{5}}{5}$.
如图,每个小正方形的边长为1,△ABC的顶点都在方格纸的格点上,则sinA=$\frac{\sqrt{5}}{5}$.