题目内容
5.关于x的一次函数y=a1x+b1与y=a2x+b2,称函数y=m(a1x+b1)+n(a2x+b2)(其中m+n=1)为这两个函数的生成函数,则当x=1时,求函数y=x+2与y=3x的生成函数的值.分析 根据新定义得到生成函数为y=(m+3n)x+2m,由于m+n=1,即n=1-m,那b=1-m代入得到生成函数为y=(3-2m)x+2m,然后计算x=1所对应的函数值即可.
解答 解:根据题意得函数y=x+2与y=3x的生成函数为y=m(x+2)+n•3x=(m+3n)x+2m,
而m+n=1,即n=1-m,
所以y=(m+3-2m)x+2m=(3-2m)x+2m,
当x=1时,y=3-2m+2m=3,
即当x=1时,求函数y=x+2与y=3x的生成函数的值为3.
点评 本题考查了一次函数的性质:k>0,y随x的增大而增大,函数从左到右上升;k<0,y随x的增大而减小,函数从左到右下降.也考查了阅读理解能力.

练习册系列答案
相关题目
15.下列可以表示y为自变量x的函数的是( )
| A. | f(x)=$\sqrt{x-2}$+$\frac{1}{\sqrt{1-x}}$ | B. | 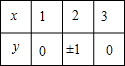 | C. |  | D. | y=1,x∈R |
 如图,已知∠AOC在∠AOB的内部,∠AOB与∠AOC互为补角,OM平分∠AOC,ON平分∠BOM,若∠NOC=40°,求∠AOB的度数.
如图,已知∠AOC在∠AOB的内部,∠AOB与∠AOC互为补角,OM平分∠AOC,ON平分∠BOM,若∠NOC=40°,求∠AOB的度数.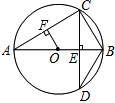 如图,AB为⊙O的直径,CD⊥AB于点E,交⊙O于点D,OF⊥AC于点F,
如图,AB为⊙O的直径,CD⊥AB于点E,交⊙O于点D,OF⊥AC于点F, 如图,在⊙O中,AB=2CD,求证:$\widehat{AB}$>2$\widehat{CD}$.
如图,在⊙O中,AB=2CD,求证:$\widehat{AB}$>2$\widehat{CD}$.